Đề số 2 - Đề kiểm tra học kì 1 - Toán 7Đáp án và lời giải chi tiết Đề số 2 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7 Quảng cáo
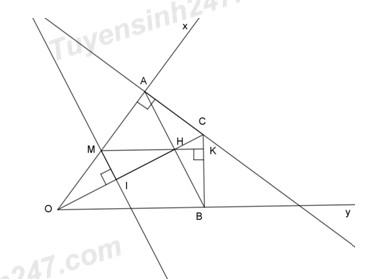
Đề bài Câu 1 (2,0 đ): Chọn chữ cái trước đáp án đúng: 1 . Trong các phân số sau, phân số nào biểu diễn số hữu tỉ\(\dfrac{3}{{ - 4}}\)? A.\(\dfrac{{20}}{{ - 15}}\) B.\(\dfrac{{20}}{{15}}\) C.\(\dfrac{{ - 12}}{{16}}\) D.\(\dfrac{{12}}{{16}}\). 2 . Kết quả so sánh 2 số\(x = \dfrac{{ - 7}}{8}\) và \(y = \dfrac{8}{{ - 9}}\) là A. x = y B. x > y C. x < y D. x = y + 1 3. Cho hàm số y = f(x) =\(1 - 2{{\rm{x}}^2}\). Giá trị của \(f\left( {\dfrac{{ - 1}}{2}} \right)\)bằng: A. 0,25 B.0 C. 0,125 D. 0,5 4. Cho x và y là hai đại lượng tỉ lệ nghịch, \(x = - \dfrac{1}{2}\)thì\(y = 4\). Hỏi x = 2 thì y bằng bao nhiêu? A. – 2 B. 2 C.– 1 D. 1 5. Giả thiết nào dưới đây suy ra được\(\Delta MNP = \Delta M'N'P'\)? A. \(\angle M = \angle M';\;MN = M'N';\;NP = N'P'\) B.\(\angle M = \angle M';\;MP = M'P';\;NP = N'P'\) C.\(\angle M = \angle M;\;\angle N = \angle N';\;\angle P = \angle P'\) D.\(\angle M = \angle M';\;MN = M'N';\;MP = M'P'\) 6. Hai tia phân giác của hai góc kề bù là: A.Hai tia trùng nhau B. Hai tia vuông góc C. Hai tia đối nhau D. Hai tia song song. 7. Nếu góc xOy = 470 thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu? A. 1330 B. 470 C.430 D. 740 8. Nếu tam giác ABC có\(\angle BAC = {50^0}\)và AB = AC thì số đo của góc ABC bằng: A.650 B. 750 C. 550 D. 450 Câu 2. (2,0 đ): 1. Thực hiện các phép tính sau: \(a)\;\sqrt {0,16} - \sqrt {\dfrac{1}{{25}}} \) \(b){\left( {\dfrac{{ - 2}}{3}} \right)^2}.\dfrac{9}{{16}} + \dfrac{1}{2}:( - 3)\) 2. Tìm x biết: \(a)\;\dfrac{3}{7} - x = \dfrac{{ - 2}}{6}\) b) \(\dfrac{{x - 1}}{{27}} = \dfrac{{ - 3}}{{1 - x}}\) Câu 3 (2,0 đ):Một mảnh vườn hình chữ nhật có chu vi là 70 m. Tỷ số giữa 2 cạnh của nó là\(\dfrac{3}{4}\). Tính diện tích của mảnh vườn hình chữ nhật đó. Câu 4 (3,0 đ): Cho góc nhọn xOy, trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi H là trung điểm của đoạn thẳng AB. a) Chứng minh:\(\Delta OAH = \Delta OBH\). b) Từ A vẽ đường thẳng vuông góc với OA, cắt tia OH tại C. Chứng minh:\(CB \bot OB\). c) Gọi I là trung điểm đoạn thẳng OH, từ I vẽ đường thẳng vuông góc với OH, cắt tia OA tại M. Kẻ HK vuông góc với BC tại K. Chứng minh: ba điểm M, H, K thẳng hàng. Câu 5 (1,0 đ): Với mọi số tự nhiên\(n \ge 2\), so sánh A với 1 biết: \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{n^2}}}\) Lời giải chi tiết Câu 1:
Câu 2: \(1.\;a)\;\sqrt {0,16} - \sqrt {\dfrac{1}{{25}}} \) \(= \sqrt {0,{4^2}} - \sqrt {{{\left( {\dfrac{1}{5}} \right)}^2}} \) \(= 0,4 - \dfrac{1}{5} = \dfrac{4}{{10}} - \dfrac{1}{5} \) \(= \dfrac{2}{5} - \dfrac{1}{5} = \dfrac{1}{5}\) \(\begin{array}{l}b){\left( {\dfrac{{ - 2}}{3}} \right)^2}.\dfrac{9}{{16}} + \dfrac{1}{2}:( - 3) \\= \dfrac{{{{( - 2)}^2}}}{{{3^2}}}.\dfrac{{{3^2}}}{{{2^4}}} + \dfrac{1}{2}.\dfrac{1}{{( - 3)}} \\= \dfrac{{{2^2}{{.3}^2}}}{{{3^2}{{.2}^{2 + 2}}}} - \dfrac{1}{{2.3}}\\ = \dfrac{{{2^2}{{.3}^2}}}{{{3^2}{{.2}^2}{{.2}^2}}} - \dfrac{1}{6} \\= \dfrac{1}{{{2^2}}} - \dfrac{1}{6} = \dfrac{1}{4} - \dfrac{1}{6}\\ = \dfrac{{1.3}}{{4.3}} - \dfrac{{1.2}}{{6.2}} = \dfrac{{3 - 2}}{{12}} = \dfrac{1}{{12}}\end{array}\) \(2.\;a)\;\dfrac{3}{7} - x = \dfrac{{ - 2}}{6} \) \(\Leftrightarrow x = \dfrac{3}{7} + \dfrac{2}{6} = \dfrac{3}{7} + \dfrac{1}{3}\) \(\Leftrightarrow x = \dfrac{{3.3}}{{7.3}} + \dfrac{{1.7}}{{3.7}}\) \(\Leftrightarrow x = \dfrac{{9 + 7}}{{21}} = \dfrac{{16}}{{21}}\) Vậy \(x = \dfrac{{16}}{{21}}\). b) \(\dfrac{{x - 1}}{{27}} = \dfrac{{ - 3}}{{1 - x}}\) (Để biểu thức có nghĩa \(\left( {1 - x} \right) \ne 0 \Leftrightarrow x \ne 1\)) \(\begin{array}{l} \Leftrightarrow (x - 1).(1 - x) = - 3.27\\ \Leftrightarrow - (1 - x).(1 - x) = - {3.3^3}\\ \Leftrightarrow - {(1 - x)^2} = - {3.3^3}\\ \Leftrightarrow {(1 - x)^2} = {3^4} = {\left( {{3^2}} \right)^2}\\ \Leftrightarrow {(1 - x)^2} = {9^2}\\ \Rightarrow \left[ \begin{array}{l}1 - x = 9\\1 - x = - 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 - 9\\x = 1 + 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 8\\x = 10\end{array} \right.(TM)\end{array}\) Vậy \(x = - 8\) hoặc \(x = 10.\) Câu 3: Gọi chiều rộng và chiều dài của mảnh vườn hình chữ nhật lần lượt là a và b (m).\(\left( {0 < a < b < 35} \right).\) Chu vi của mảnh vườn hình chữ nhật là 70 m, ta có: 2(a + b) = 70 \( \Leftrightarrow \)a + b = 35 Tỉ số giữa 2 cạnh của nó là \(\dfrac{3}{4}\), suy ra: \(\dfrac{a}{b} = \dfrac{3}{4} \Leftrightarrow \dfrac{a}{3} = \dfrac{b}{4}\) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{{a + b}}{{3 + 4}} = \dfrac{{35}}{7} = 5.\\ \Rightarrow \left\{ \begin{array}{l}a = 5.3 = 15\;\;\left( {tm} \right)\\b = 5.4 = 20\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\) Vậy chiều rộng và chiều dài của mảnh vườn hình chữ nhật lần lượt là 15 (m) và 20 (m).\(\) Câu 4: a) Xét \(\Delta OAH\) và \(\Delta OBH\) ta có: OA = OB (theo giả thiết) HA = HB (H là trung điểm AB) OH chung \( \Rightarrow \Delta OAH = \Delta OBH\;\;\left( {c - c - c} \right)\) b) Ta có: \(\Delta OAH = \Delta OBH\) (chứng minh trên) \( \Rightarrow \angle AOH = \angle BOH\) ( 2 góc tương ứng bằng nhau) Hay \(\angle AOC = \angle BOC\) Xét \(\Delta OAC\) và \(\Delta OBC\) ta có: OA = OB (theo giả thiết) OC chung \(\angle AOC = \angle BOC\) \( \Rightarrow \Delta OAC = \Delta OBC\;\;\left( {c - g - c} \right)\) \( \Rightarrow \angle OAC = \angle OBC\)(2 góc tương ứng) Mà \(\angle OAC\)= 900 nên \(\angle OBC\) = 900 \( \Rightarrow CB \bot OB\)( điều phải chứng minh) c) Ta có: \(\angle AOC = \angle BOC\) (chứng minh trên) (1) Xét 2 tam giác vuông MIO và MIH ta có: MI chung IO = IH (Vì I là trung điểm của OH) \( \Rightarrow \Delta MI{\rm{O}} = \Delta MIH\) (Cạnh góc vuông – cạnh góc vuông) \( \Rightarrow \angle MOI = \angle MHI\) (2 góc tương ứng) \(Hay\;\angle AOC = \angle MHI\) (2) Từ (1) và (2) ta có: \(\angle BOC = \angle MHI\) (cặp góc ở vị trí so le trong) \( \Rightarrow MH//OB\) (*) Lại có: \(\left. \begin{array}{l}HK \bot BC\\OB \bot BC\end{array} \right\} \Rightarrow HK//OB\) (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**) Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB. Suy ra M, H, K thẳng hàng (điều phải chứng minh) Câu 5: \(A = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{n^2}}} < \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + .. + \dfrac{1}{{(n - 1).n}}\) \(\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + .. + \dfrac{1}{{(n - 1).n}} \)\(\;= \dfrac{1}{1} - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{n - 1}} - \dfrac{1}{n} \)\(\;= \dfrac{1}{1} - \dfrac{1}{n} = 1 - \dfrac{1}{n} < 1\) (Vì \(n \ge 2\)) Vậy A < 1. Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 7 tại Tuyensinh247.com Loigiaihay.com
|