Đề kiểm tra giữa kì I Toán 6 - Đề số 5 có lời giải chi tiết

Đề bài

Phần I: Trắc nghiệm (2,0 điểm)

Hãy chọn và viết vào bài làm một trong các chữ \(A,\,\,B,\,\,C,\,\,D\) đứng trước phương án đúng.

Câu 1. Tập hợp các số tự nhiên khác \(0\) và không vượt quá \(5\) là:

A. \(\left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\)                        B. \(\left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\)   C. \(\left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\)                                      D. \(\left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}\)

Câu 2. Số phần tử của tập hợp \(A = \left\{ {1991;\,\,1992; \ldots ;\,\,2019;\,\,2020} \right\}\) là:

A. \(28\)                             B. \(29\)                                  C. \(30\)                                  D. \(31\)

Câu 3. Một tàu hỏa chở \(512\) hành khách. Biết rằng mỗi toa có \(10\) khoang, mỗi khoang có \(4\) chỗ ngồi. Cần ít nhất mấy toa để chở hết số hành khách?

A. \(12\)                             B. \(13\)                                  C. \(14\)                                  D. \(15\)

Câu 4. Trong các số \(142;\,\,255;\,\,197;\,\,210\). Số không chia hết cho cả \(2\) và \(5\) là:

A. \(142\)                           B. \(255\)                                C. \(210\)                                D. \(197\)

Câu 5. Phép tính đúng là:

A. \({2019^0} = 0\)            B. \({x^2}.x = {x^3}\)            C. \({2^5}:{2^2} = {2^7}\)     D. \(10000 = {10^3}\)

Câu 6. Với \(x = 2,\,\,y = 3\) thì \({x^2}{y^2}\) có giá trị là:

A. \(36\)                             B. \(27\)                                  C. \(72\)                                  D. \(108\)

Câu 7. Cho hình vẽ:

Chọn khẳng định đúng trong các câu sau:

A. \(A \in a,\,\,B \notin b\)                                               B. \(A \in a,\,\,B \in b\)           C. \(A \notin a,\,\,B \notin b\)                                           D. \(A \notin a,\,\,B \in b\)

Câu 8. Số La Mã \(XIV\) có giá trị là:

A. \(17\)                             B. \(16\)                                  C. \(15\)                                  D. \(14\)

Phần II: Tự luận (8,0 điểm)

Câu 9 (2,5 điểm): Thực hiện phép tính (tính nhanh nếu có thể)

a) \(146 + 121 + 54 + 379\)                                                   b) \(43.17 + 29.57 + 13.43 + 57\)

c) \({5^6}:{5^4} + {3^2} - {2019^0}\)                                                                                  d) \(100:\left\{ {250:\left[ {450 - \left( {{{4.5}^3} - {2^3}.25} \right)} \right]} \right\}\) 

Câu 10 (2,5 điểm): Tìm số tự nhiên \(x,\) biết:

a)                                                                         b) \(x - 280:35 = 5.54\)

c) \(390:\left( {5x - 5} \right) = 39\)                                                                                     d) \(6{x^3} - 8 = 40\)

Câu 11 (2 điểm): Cho đường thẳng \(mn,\)  lấy điểm \(O\) thuộc đường thẳng \(mn\) và điểm \(A\) không thuộc đường thẳng \(mn.\) Vẽ tia \(OA\), lấy điểm \(C\) sao cho \(A\) nằm giữa \(O\) và \(C\).

a) Kể tên các tia đối nhau gốc \(O\), các tia trùng nhau gốc \(O\).

b) Hai tia \(OA\) và \(AC\) có trùng nhau không? Vì sao?

Câu 12 (1,0 điểm):

a) Cho \(S = 1 + 3 + {3^2} + {3^3} +  \ldots  + {3^{98}} + {3^{99}}\). Tìm chữ số tận cùng của \(S\).

b) Tìm các số tự nhiên \(x,\,\,y\) sao cho: \({7^x} + {12^y} = 50\)

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

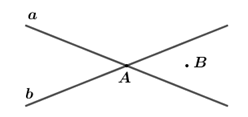
Câu 1:

Phương pháp:

Liệt kê tất cả các số tự nhiên khác và không vượt quá \(5\).

Cách giải:

Các số tự nhiên khác \(0\)và không vượt quá \(5\) là: \(1;\,\,2;\,\,3;\,\,4;\,\,5\)

Vậy tập hợp các số tự nhiên khác \(0\) và không vượt quá \(5\) là: \(\left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5} \right\}.\)

Chọn D.

Câu 2:

Phương pháp:

Áp dụng công thức tìm số số hạng của dãy số: Số số hạng = (Số cuối – Số đầu) : Khoảng cách giữa hai số + 1

Cách giải:

Số phần tử của tập hợp \(A\) là: \(\left( {2020 - 1991} \right):1 + 1 = 30\) (phần tử)

Chọn C.

Câu 3:

Phương pháp:

Tính số chỗ ngồi ở mỗi toa và thực hiện phép tính chia, còn dư bao nhiêu hành khách thì xếp vào \(1\) toa nữa.

Cách giải:

Mỗi toa có số chỗ ngồi là: \(4.10 = 40\) (chỗ ngồi)

Để chở \(512\) hành khách cần số toa là: \(512:40 = 12\) (toa) và dư \(32\) hành khách.

\(32\) hành khách được xếp vào \(1\) toa nữa.

Vậy cần ít nhất \(12 + 1 = 13\) toa để chở hết hành khách.

Chọn B.

Câu 4:

Phương pháp:

Xét từng đáp án và áp dụng dấu hiệu chia hết cho \(2\) và cho \(5\)

Cách giải:

+) Vì \(142\) có chữ số tận cùng là \(2\) nên \(142\) chỉ chia hết cho \(2\) mà không chia hết cho \(5\).

+) Vì \(255\) có chữ số tận cùng là \(5\) nên \(255\) chỉ chia hết cho \(5\) mà không chia hết cho \(2\).

+) Vì \(210\) có chữ số tận cùng là \(0\) nên \(210\) chia hết cho cả \(5\) và \(2\).

+) Vì \(197\) có chữ số tận cùng là \(7\) nên \(197\) không chia hết cho cả \(5\) và \(2\).

Chọn D.

Câu 5:

Phương pháp:

Xét từng đáp án và áp dụng các phép toán của lũy thừa.

Cách giải:

Ta có:

+) \({2019^0} = 1 \Rightarrow \) Đáp án A sai.

+) \({x^2}.x = {x^{2 + 1}} = {x^3} \Rightarrow \) Đáp án B đúng.

+) \({2^5}:{2^2} = {2^{5 - 2}} = {2^3} \Rightarrow \) Đáp án C sai.

+) \(10000 = {10^4} \Rightarrow \) Đáp án D sai.

Chọn B.

Câu 6:

Phương pháp:

Thay \(x,\,\,y\) để tính giá trị của biểu thức \({x^2}{y^2}\).

Cách giải:

Thay \(x = 2,\,\,y = 3\) vào biểu thức \({x^2}{y^2}\) ta được: \({x^2}{y^2} = {2^2}{.3^2} = 4.9 = 36\)

Chọn A.

Câu 7:

Phương pháp:

Quan sát hình vẽ, xác định vị trí của điểm \(A,\,\,B\) so với đường thẳng \(a,\,\,b\).

Cách giải:

Vì \(A\) nằm trên đường thẳng \(a\) nên \(A \in a\).

Vì \(B\) không nằm trên đường thẳng \(b\) nên \(B \notin b\).

Vậy \(A \in a,\,\,B \notin b\).

Chọn A.

Câu 8:

Phương pháp:

Áp dụng cách đọc và viết số La Mã.

Cách giải:

Số La Mã \(XIV\) có giá trị là \(14\).

Chọn D.

II. TỰ LUẬN

Câu 9:

Phương pháp:

Áp dụng các công thức về lũy thừa, thứ tự thực hiện phép tính và các tính chất của các phép toán.

Cách giải:

Câu 10:

Phương pháp:

+) Sử dụng quy tắc Chuyển vế - đổi dấu.

+) Ta có: \({x^m} = {a^m}\,\) \( \Rightarrow x = a.\)

Cách giải:

Câu 11:

Phương pháp:

Áp dụng các định nghĩa của hai tia đối nhau và hai tia trùng nhau.

Cách giải:

a) Kể tên các tia đối nhau gốc \(O\), các tia trùng nhau gốc \(O\).

Các tia đối nhau gốc \(O\) là: \(Om\) và \(On\)

Các tia trùng nhau gốc \(O\) là: \(OA\) và \(OC\).

b) Hai tia \(OA\) và \(AC\) có trùng nhau không? Vì sao?

Hai tia \(OA\) và \(AC\) không phải là hai tia trùng nhau vì hai tia này không chung gốc.

Câu 12:

Phương pháp:

a) Tính \(3S - S\) để tìm được tổng \(S\).

b) Xét \({12^2} > 50\) nên để có \({7^x} + {12^y} = 50\) thì \(y < 2\) và \(y\) là số tự nhiên. Xét từng trường hợp của \(y\) để tìm \(x\).

Cách giải:

a) Cho \(S = 1 + 3 + {3^2} + {3^3} +  \ldots  + {3^{98}} + {3^{99}}\). Tìm chữ số tận cùng của \(S\).

Ta có: \(S = 1 + 3 + {3^2} + {3^3} +  \ldots  + {3^{98}} + {3^{99}}\)

\( \Rightarrow 3S = 3 + {3^2} + {3^3} +  \ldots  + {3^{99}} + {3^{100}}\)

\( \Rightarrow 3S - S = \left( {3 + {3^2} + {3^3} +  \ldots  + {3^{99}} + {3^{100}}} \right) - \left( {1 + 3 + {3^2} + {3^3} +  \ldots  + {3^{98}} + {3^{99}}} \right)\)

\( \Rightarrow 2S = {3^{100}} - 1\)

\( \Rightarrow S = \frac{{{3^{100}} - 1}}{2}\)

Vì \({3^4}\) có chữ số tận cùng là \(1\) nên \({\left( {{3^4}} \right)^{25}}\) có chữ số tận cùng là \(1\).

\( \Rightarrow {3^{100}} - 1\) có chữ số tận cùng là \(0\)

\( \Rightarrow S\)có chữ số tận cùng là \(5\).

b) Tìm các số tự nhiên \(x,\,\,y\) sao cho: \({7^x} + {12^y} = 50\)

Ta có: \({7^x} + {12^y} = 50\)

Vì \({12^2} = 144 > 50\) suy ra \(y < 2\).

Vì \(y\) là số tự nhiên nên \(y \in \left\{ {0;\,\,1} \right\}\).

+) Với \(y = 0\) ta có: \({7^x} + {12^0} = 50 \Rightarrow {7^x} = 49 \Rightarrow x = 2\) (thỏa mãn)

+) Với \(y = 1\) ta có: \({7^x} + {12^1} = 50 \Rightarrow {7^x} = 38 \Rightarrow \) Không có giá trị nào của \(x\) thỏa mãn.

Vậy \(\left( {x;\,\,y} \right) = \left( {2;\,\,0} \right)\).