Đề kiểm tra giữa kì 1 Toán 10 đề số 2

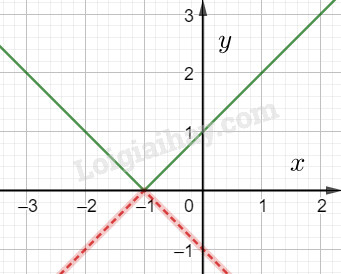
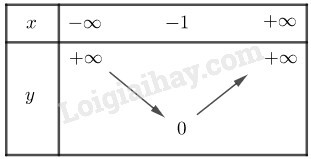
Đề bài

Câu 1.(2,5 điểm)

a) Xét tính đúng sai và lập mệnh đề phủ định của mệnh đề sau:

$\forall a \in \mathbb{R},a\left( {a + 1} \right)$ không chia hết cho 2.

b) Tìm tập xác định của hàm số $y = \sqrt {x + 3}  + \dfrac{{2{x^2} + 2}}{{\left| { - {x^2} + 5x + 6} \right|}}$

c) Xét tính chẵn lẻ của hàm số $y = 2021{x^{2021}} + 2019x\left| x \right| + 5$

Câu 2.(2 điểm)

a) Tìm $m \in \left[ {1;2020} \right]$ để hàm số $y = \left( {{m^2} - 4} \right)x + m - 1$ đồng biến trên $\mathbb{R}$.

b) Vẽ đồ thị và lập bảng biến thiên hàm số $y = \left| {x + 1} \right|$

Câu 3. (2 điểm) Gọi $(P)$ là đồ thị của hàm số $y = {x^2} + ax + b$ đi qua gốc tọa độ và có trục đối xứng là $x = 2$.

a) Tìm $a,b$.

b) Khi tịnh tiến đồ thị $\left( P \right)$ sang trái 1 đơn vị, rồi xuống dưới 3 đơn vị thì ta được đồ thị của hàm số nào?

Câu 4.(3,5 điểm) Cho tam giác ABC nội tiếp đường tròn tâm O bán kính R. Gọi G là trọng tâm tam giác ABC, F là điểm xác định bởi $4\overrightarrow {AF}  = \overrightarrow {AB}$.

1) Phân tích vectơ $\overrightarrow {AF}$ theo hai vectơ $\overrightarrow {AC}$ và $\overrightarrow {BC}$.

2) Tìm số thực x sao cho $\overrightarrow {BH}  = x\overrightarrow {BC}$ đồng thời ba điểm F, H, G thẳng hàng.

3) Với mỗi điểm M, xác định điểm N thỏa mãn: $\overrightarrow {MN}  = \dfrac{2}{3}\left( {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} } \right)$. Tìm tập hợp các điểm N khi M chạy trên đường tròn tâm O bán kính R.

Lời giải chi tiết

Câu 1.

a) Mệnh đề sai vì:

$a = 1 \in \mathbb{R} \Rightarrow a\left( {a + 1} \right) = 2$ chia hết cho 2.

Mệnh đề phủ định: $\exists a \in \mathbb{R},a\left( {a + 1} \right)$ chia hết cho 2.

b) ĐKXĐ: $\left\{ \begin{array}{l}x + 3 \ge 0\\ - {x^2} + 5x + 6 \ne 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x \ge  - 3\\x \ne 6\\x \ne  - 1\end{array} \right.$

Tập xác định của hàm số là: $D = \left[ { - 3; - 1} \right) \cup \left( { - 1;6} \right) \cup \left( {6; + \infty } \right)$

c) Tập xác định $D = \mathbb{R}$

$\forall x \in D \Rightarrow  - x \in D$

Lấy tùy ý $x \in D$ ta có

$\begin{array}{l}f\left( { - x} \right) = 2021{\left( { - x} \right)^{2021}} + 2021\left( { - x} \right)\left| { - x} \right| + 5\\ =  - 2021{x^{2021}} - 2021x\left| x \right| + 5\end{array}$

$\Rightarrow f\left( { - x} \right) \ne f\left( x \right)$ và $f\left( { - x} \right) \ne f\left( x \right)$

Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.

Câu 2.

a) Hàm số $y = \left( {{m^2} - 4} \right)x + m - 1$ đồng biến trên $\mathbb{R}$

$\begin{array}{l} \Leftrightarrow {m^2} - 4 > 0\forall x \in \mathbb{R}\\ \Leftrightarrow \left( {m - 2} \right)\left( {m + 2} \right) > 0\forall x \in \mathbb{R}\\ \Leftrightarrow \left[ \begin{array}{l}m > 2\\m <  - 2\end{array} \right.\end{array}$

Kết hợp với điều kiện $1 \le m \le 2020$. Ta được:

$\left\{ \begin{array}{l}1 \le m \le 2020\\\left[ \begin{array}{l}m > 2\\m <  - 2\end{array} \right.\end{array} \right. \Leftrightarrow 2 < m \le 2020$

Vậy $2 < m \le 2020$.

b) Ta có hàm số $y = \left| {x + 1} \right|$ xác định với mọi $x$.

Nếu $x \ge  - 1$, thì $\left| {x + 1} \right| = x + 1$

Nếu $x <  - 1$, thì $\left| {x + 1} \right| =  - x - 1$

Do đó hàm số đã cho là $y = \left\{ \begin{array}{l}x + 1{\rm{ khi }}x \ge  - 1\\ - x - 1{\rm{ khi }}x <  - 1\end{array} \right.$

Đồ thị:

Hàm số đồng biến trên $\left( { - 1; + \infty } \right)$ và nghịch biến trên $\left( { - \infty ; - 1} \right)$

Bảng biến thiên:

Câu 3.

a) Ta có $(P)$ đi qua gốc tọa độ O(0;0)  nên tọa độ của O thỏa mãn hàm số $y = {x^2} + ax + b$.

$\Rightarrow 0 = {0^2} + a.0 + b \Leftrightarrow b = 0$.

$(P)$ có trục đối xứng là $x =  - \dfrac{a}{2}$$\Rightarrow  - \dfrac{a}{2} = 2 \Leftrightarrow a =  - 4$.

Vậy $a =  - 4,b = 0$.

b) Hàm số ban đầu là: $y = {x^2} - 4x$.

Khi tịnh tiến đồ thị sang trái 1 đơn vị ta được đồ thị của hàm số

$y = f\left( {x + 1} \right) = {\left( {x + 1} \right)^2} - 4\left( {x + 1} \right) = {x^2} - 2x - 3$.

Khi tịnh tiến đồ thị trên xuống dưới 3 đơn vị ta được đồ thị của hàm số

$y = {x^2} - 2x - 3 - 3 = {x^2} - 2x - 6$.

Vậy hàm số cần tìm là $y = {x^2} - 2x - 6$.

Câu 4.

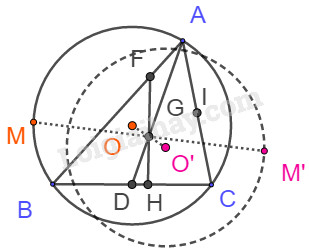
a) Ta có

$\begin{array}{l}4\overrightarrow {{\rm{AF}}}  = \overrightarrow {AB}  \Rightarrow \overrightarrow {{\rm{AF}}}  = \dfrac{1}{4}\overrightarrow {AB} \\ = \dfrac{1}{4}\left( {\overrightarrow {AC}  - \overrightarrow {BC} } \right) = \dfrac{1}{4}\overrightarrow {AC}  - \dfrac{1}{4}\overrightarrow {BC} \end{array}$

b) Gọi D là trung điểm BC. Vì H thuộc cạnh BC nên đặt $\overrightarrow {BH}  = x\overrightarrow {BC}$.

Ta có :

$\begin{array}{l}\overrightarrow {FG}  = \overrightarrow {FA}  + \overrightarrow {AG}  =  - \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AD} \\ =  - \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{2}{3}.\dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\\ = \dfrac{1}{{12}}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AC} \end{array}$

$\begin{array}{l}\overrightarrow {FH}  = \overrightarrow {FB}  + \overrightarrow {BH}  =  - \dfrac{3}{4}\overrightarrow {AB}  + x\overrightarrow {BC} \\ =  - \dfrac{3}{4}\overrightarrow {AB}  + x\overrightarrow {AC}  - x\overrightarrow {AB} \\ = \left( { - x - \dfrac{3}{4}} \right)\overrightarrow {AB}  + x\overrightarrow {AC} \end{array}$

Để F,G, H thẳng hàng thì tồn tại số k khác 0 để $\overrightarrow {FG}  = k\overrightarrow {FH}$

$\Leftrightarrow \dfrac{1}{{12}}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AC}  = k\left[ {\left( { - x - \dfrac{3}{4}} \right)\overrightarrow {AB}  + x\overrightarrow {AC} } \right]$

$\Leftrightarrow \left\{ \begin{array}{l} - kx - \dfrac{3}{4}k = \dfrac{1}{{12}}\\kx = \dfrac{1}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k =  - \dfrac{5}{9}\\x =  - \dfrac{3}{5}\end{array} \right.$

Vậy $x =  - \dfrac{3}{5}$.

c) $G$ là trọng tâm tam giác $ABC$ nên ta có:

$\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG}$$\Rightarrow \overrightarrow {MN}  = \dfrac{2}{3}.3\overrightarrow {MG}  = 2\overrightarrow {MG}$.

Hay $N$ là điểm đối xứng với $M$ qua $G$ $\Rightarrow \overrightarrow {GN}  = \overrightarrow {MG}$

Gọi $O'$ là điểm đối xứng với $O$ qua $G$ $\Rightarrow \overrightarrow {GO'}  = \overrightarrow {OG}$

Khi đó $\overrightarrow {NO'}  = \overrightarrow {OM}  \Rightarrow O'N = OM = R$. Vì O và G cố định nên O’ cố định, do đó khi M chạy trên đường tròn tâm $O$ bán kính R thì $N$ chạy trên đường tròn tâm $O'$ bán kính R.

Loigiaihay.com