Đề thi giữa kì 1 Toán 12 - Đề số 3Đề bài
Câu 1 :
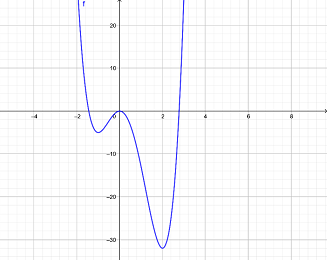
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
Câu 2 :
Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ , khi đó:
Câu 3 :
Hàm số \(y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\) nghịch biến trên khoảng nào dưới đây?
Câu 4 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:
Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
Câu 5 :
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng: 
Câu 6 :
Chọn mệnh đề đúng:
Câu 7 :
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
Câu 8 :
Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng: “Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”
Câu 9 :
Tính giá trị của biểu thức \(P = {\left( {2\sqrt 6 - 5} \right)^{2020}}{\left( {2\sqrt 6 + 5} \right)^{2021}}\).
Câu 10 :
Khối mười hai mặt đều là khối đa diện đều loại:
Câu 11 :
Tính giá trị \({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}},\)ta được kết quả là:
Câu 12 :
Biết đồ thị các hàm số $y = {x^3} + \dfrac{5}{4}x - 2$ và $y = {x^2} + x - 2$ tiếp xúc nhau tại điểm $M({x_0}\,;\,{y_0})$. Tìm ${x_0}.$
Câu 13 :
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng: 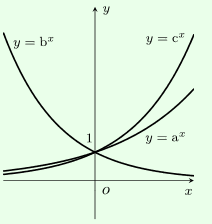
Câu 14 :
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng? 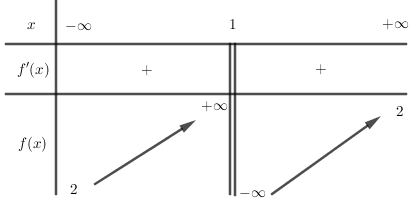
Câu 15 :
Chọn kết luận đúng:
Câu 16 :
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau: 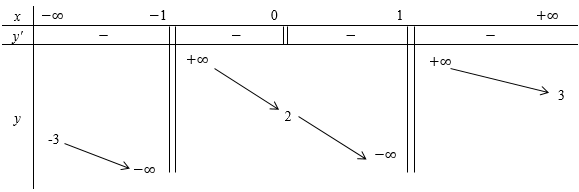 Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Câu 17 :
Số mặt phẳng đối xứng của mặt cầu là:
Câu 18 :
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên: 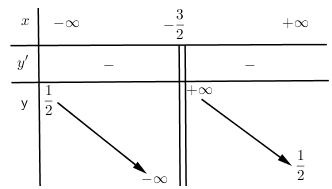 Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
Câu 19 :
Tính giá trị của biểu thức \({3^2}{.5^{2 + 2\sqrt 2 }}:{25^{\left( {1 + \sqrt 2 } \right)}}\) có kết quả là:
Câu 20 :
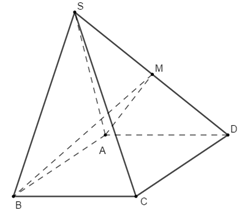
Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
Câu 21 :
Cho $n \in Z, n>0$, với điều kiện nào của $a$ thì đẳng thức sau xảy ra: ${a^{ - n}} = \dfrac{1}{{{a^n}}}$?
Câu 22 :
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Câu 23 :
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
Câu 24 :
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
Câu 25 :
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
Câu 26 :
Công thức nào sau đây là công thức tăng trưởng mũ?
Câu 27 :
Trong các hình dưới đây, hình nào là khối đa diện? 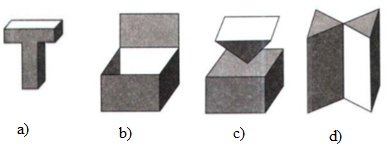
Câu 28 :
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai? 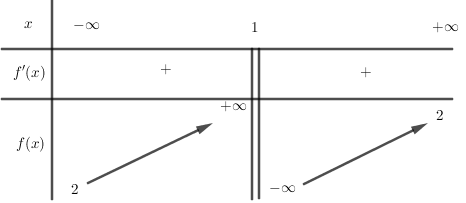
Câu 29 :
Hàm số nào sau đây có đồ thị như hình vẽ? 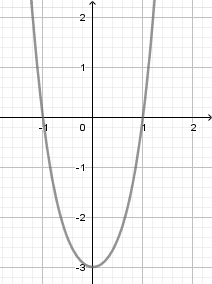
Câu 30 :
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
Câu 31 :
Cho hàm số: $f(x) = - 2{x^3} + 3{x^2} + 12x - 5.$ Trong các mệnh đề sau, tìm mệnh đề sai?
Câu 32 :
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Câu 33 :
Cho hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.$ Tìm $m$ để đồ thị hàm số có hai điểm cực trị là $A, B$ sao cho đường thẳng $AB$ vuông góc với $d:\,x - y - 9 = 0$
Câu 34 :
Đồ thị hàm số $y = \dfrac{{x - 3}}{{{x^2} + x - 2}}$ có bao nhiêu đường tiệm cận đứng?
Câu 35 :
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng: 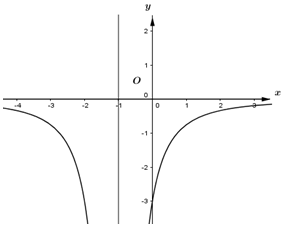
Câu 36 :
Cho hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có bảng biến thiên: 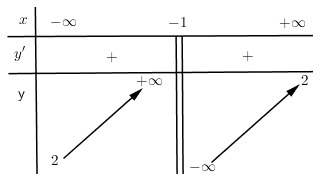 Giá trị của ${c^2} - {d^2}$ bằng:
Câu 37 :
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Câu 38 :
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
Câu 39 :
Số \(9465779232\) có bao nhiêu ước số nguyên dương?
Câu 40 :
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Câu 41 :
Cho các phát biểu sau: (I). Nếu \(C = \sqrt {AB} \) thì \(2\ln C = \ln A + \ln B\) với $A, B$ là các biểu thức luôn nhận giá trị dương. (II). \(\left( {a - 1} \right){\log _a}x \ge 0 \Leftrightarrow x \ge 1\) với \(a > 0,a \ne 1\) (III). \({m^{{{\log }_a}m}} = {n^{{{\log }_a}n}},\) với \(m,n > 0\) và \(a > 0,a \ne 1\) (IV).\(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty \) Số phát biểu đúng là
Câu 42 :
Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\).
Câu 43 :
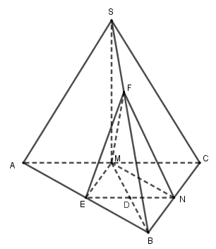
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng
Câu 44 :
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy $ABCD$ là hình chữ nhật với \(AB = \sqrt 3 ,AD = \sqrt 7 \). Hai mặt bên $\left( {ABB'A'} \right)$ và $\left( {ADD'A'} \right)$ lần lượt tạo với đáy những góc \({45^0}\) và \({60^0}\). Tính thể tích khối hộp nếu biết cạnh bên bằng $1$.
Câu 45 :
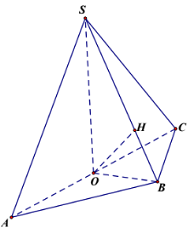
Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
Câu 46 :
Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
Câu 47 :
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?
Câu 48 :
Cho hàm số \(y = \dfrac{x}{{1 - x}}\,\,\left( C \right)\) và điểm \(A\left( { - 1;1} \right)\). Tìm \(m\) để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) sao cho \(A{M^2} + A{N^2}\) đạt giá trị nhỏ nhất.
Câu 49 :
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên 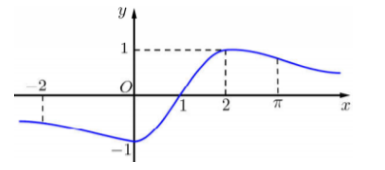 Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
Câu 50 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).
Lời giải và đáp án
Câu 1 :
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
Đáp án : B Lời giải chi tiết :
Đồ thị hàm bậc 4 trùng phương luôn cắt trục tung tại điểm $\left( {0;c} \right)$ chính là cực trị của đồ thị hàm số. Ngoài ra, đồ thị hàm số bậc 4 trùng phương cũng có thể không cắt $Ox$ nên A sai. Đồ thị nhận trục tung làm trục đối xứng chứ không phải trục hoành nên C sai. Đồ thị không có tâm đối xứng nên D sai.
Câu 2 :
Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ , khi đó:
Đáp án : D Phương pháp giải :
Hàm số $y = f\left( x \right)$ có $\mathop {\lim }\limits_{x \to + \infty } = + \infty ;\mathop {\lim }\limits_{x \to - \infty } = - \infty $ thì không có GTLN, GTNN. Lời giải chi tiết :
Hàm số $y = f\left( x \right)$ có $\mathop {\lim }\limits_{x \to + \infty }f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ thì không có GTLN, GTNN trên $R$ vì không tồn tại số $M,m$ để $f\left( x \right) \leqslant M,f\left( x \right) \geqslant m,\forall x \in R$.
Câu 3 :
Hàm số \(y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\) nghịch biến trên khoảng nào dưới đây?
Đáp án : A Phương pháp giải :
Hàm số \(y = {\log _a}f\left( x \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0.\) Hàm số \(y = {\log _a}f\left( x \right)\) nghịch biến trên TXĐ \( \Leftrightarrow 0 < a < 1.\) Lời giải chi tiết :
Xét hàm số \(y = {\log _{\frac{e }{3}}}\left( {x - 1} \right)\) có TXĐ: \(D = \left( {1; + \infty } \right)\) và \(a = \frac{e }{3} < 1\) \( \Rightarrow \) Hàm số nghịch biến trên \(\left( {1; + \infty } \right).\)
Câu 4 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:
Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
Đáp án : A Phương pháp giải :
Dựa vào đồ thị hàm số suy ra các khoảng đồng biến và nghịch biến của hàm số \(y = f\left( x \right)\) từ đó suy ra tính đồng biến và nghịch biến của hàm số \(y = - 2f\left( x \right).\) Lời giải chi tiết :
Dựa vào đồ thị hàm số ta có hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { - \infty ;\,0} \right)\) và \(\left( {2;\, + \infty } \right).\) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;\,\,2} \right).\) Xét hàm số: \(y = - 2f\left( x \right)\) ta có: \(y' = - 2f'\left( x \right).\) Hàm số đồng biến \( \Leftrightarrow - 2f'\left( x \right) \ge 0 \Leftrightarrow f'\left( x \right) \le 0 \Leftrightarrow 0 \le x \le 2.\) Vậy hàm số \(y = - 2f\left( x \right)\) đồng biến \( \Leftrightarrow x \in \left[ {0;\,2} \right].\)
Câu 5 :
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng: 
Đáp án : D Phương pháp giải :
Sử dụng các dáng đồ thị hàm số \(y = {x^\alpha }\) ứng với các điều kiện khác nhau của \(\alpha \): 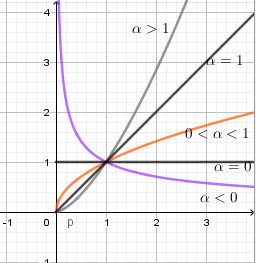 Lời giải chi tiết :
Từ hình vẽ ta thấy \(1 < {2^\alpha } < 2 \Rightarrow 0 < \alpha < 1\) .
Câu 6 :
Chọn mệnh đề đúng:
Đáp án : A Phương pháp giải :
Sử dụng công thức ${\log _a}{a^b} = b$ với $0<a\ne 1$. Lời giải chi tiết :
Ta có: ${\log _2}16 = {\log _2}{2^4} = 4$; ${\log _3}81 = {\log _3}{3^4} = 4$ nên ${\log _2}16 = {\log _3}81$.
Câu 7 :
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
Đáp án : A Lời giải chi tiết :
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là tâm đối xứng của đồ thị hàm số.
Câu 8 :
Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng: “Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”
Đáp án : D Phương pháp giải :
Sử dụng phương pháp chọn điểm rơi, lấy ví dụ cho hình tứ diện để chọn đáp án. Lời giải chi tiết :
Hình tứ diện có \(6\) cạnh và \(4\) đỉnh nên số cạnh của tứ diện lớn hơn số mặt của nó.
Câu 9 :
Tính giá trị của biểu thức \(P = {\left( {2\sqrt 6 - 5} \right)^{2020}}{\left( {2\sqrt 6 + 5} \right)^{2021}}\).
Đáp án : D Phương pháp giải :
- Áp dụng công thức \({a^m}.{b^m} = {\left( {ab} \right)^m}.\) - Sử dụng hằng đẳng thức \(\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}\). Lời giải chi tiết :
\(\begin{array}{l}P = {\left( {2\sqrt 6 - 5} \right)^{2020}}{\left( {2\sqrt 6 + 5} \right)^{2021}}\\\,\,\,\,\, = {\left[ {\left( {2\sqrt 6 - 5} \right)\left( {2\sqrt 6 + 5} \right)} \right]^{2020}}.\left( {2\sqrt 6 + 5} \right)\\\,\,\,\, = {\left( {24 - 25} \right)^{2020}}.\left( {2\sqrt 6 + 5} \right) = 2\sqrt 6 + 5\end{array}\)
Câu 10 :
Khối mười hai mặt đều là khối đa diện đều loại:
Đáp án : C Lời giải chi tiết :
Khối mười hai mặt đều thuộc loại \(\left\{ {5;3} \right\}\).
Câu 11 :
Tính giá trị \({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}},\)ta được kết quả là:
Đáp án : A Phương pháp giải :
Sử dụng công thức \(\dfrac{1}{{{x^m}}} = {x^{ - m}},\,\,{\left( {{x^m}} \right)^n} = {x^{mn}}\). Lời giải chi tiết :
\({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}} = {16^{0,75}} + {8^{\frac{4}{3}}} = {\left( {{2^4}} \right)^{\frac{3}{4}}} + {\left( {{2^3}} \right)^{\frac{4}{3}}} = {2^3} + {2^4} = 24\).
Câu 12 :
Biết đồ thị các hàm số $y = {x^3} + \dfrac{5}{4}x - 2$ và $y = {x^2} + x - 2$ tiếp xúc nhau tại điểm $M({x_0}\,;\,{y_0})$. Tìm ${x_0}.$
Đáp án : B Phương pháp giải :
- Điều kiện để hai đường cong tiếp xúc là hệ phương trình $\left\{ \begin{gathered} f\left( x \right) = g\left( x \right) \hfill \\ f'\left( x \right) = g'\left( x \right) \hfill \\ \end{gathered} \right.$ có nghiệm. - Giải hệ trên tìm $x$. Lời giải chi tiết :
Hoành độ tiếp điểm của hai đồ thị hàm số là nghiệm của hệ phương trình: \(\begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f'\left( x \right) = g'\left( x \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^3} + \dfrac{5}{4}x - 2 = {x^2} + x - 2\\3{x^2} + \dfrac{5}{4} = 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^3} - {x^2} + \dfrac{1}{4}x = 0\\3{x^2} - 2x + \dfrac{1}{4} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = \dfrac{1}{2}\end{array} \right.\\\left[ \begin{array}{l}x = \dfrac{1}{2}\\x = \dfrac{1}{6}\end{array} \right.\end{array} \right. \Leftrightarrow x = \dfrac{1}{2}\end{array}\) Vậy $x = \dfrac{1}{2}$ là hoành độ điểm tiếp xúc.
Câu 13 :
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng: 
Đáp án : A Phương pháp giải :
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số. + Hàm số đồng biến thì cơ số lớn hơn \(1\). + Hàm số nghịch biến thì cơ số lớn hơn \(0\) và nhỏ hơn \(1\). - Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số. - Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm. Lời giải chi tiết :
Ta thấy: - Hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\). - Hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1 > b\), loại B và D. - Xét phần đồ thị hai hàm số \(y = {a^x},y = {c^x}\) ta thấy phần đồ thị hàm số \(y = {c^x}\) nằm trên đồ thị hàm số \(y = {a^x}\) nên \({c^x} > {a^x},\forall x > 0 \Leftrightarrow c > a\).
Câu 14 :
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng? 
Đáp án : C Phương pháp giải :
Quan sát bảng biến thiên và tìm các tiệm cận ngang, tiệm cận đứng của đồ thị hàm số. Lời giải chi tiết :
Vì $\mathop {\lim }\limits_{x \to \pm \infty } y = 2$ nên $y = 2$ là tiệm cận ngang của đồ thị hàm số. Vì $\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty $ nên $x = 1$ là tiệm cận đứng của đồ thị hàm số.
Câu 15 :
Chọn kết luận đúng:
Đáp án : A Phương pháp giải :
Nhận xét giao điểm của các loại đồ thị hàm số bậc ba với trục hoành và kết luận. Lời giải chi tiết :
- Hàm số bậc ba không có cực trị thì nó đơn điệu tăng hoặc giảm trên $R$ nên đồ thị luôn cắt trục hoành tại $1$ điểm duy nhất nên A đúng, D sai. - Hàm số bậc ba có 2 cực trị thì đồ thị có thể cắt trục hoành tại $1,2$ hoặc $3$ điểm nên B, C sai.
Câu 16 :
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:  Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Đáp án : C Phương pháp giải :
- Biện luận số nghiệm của phương trình dựa vào số giao điểm của đường thẳng và đường cong vừa vẽ được. Lời giải chi tiết :
Quan sát BBT ta thấy đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt $ \Leftrightarrow \left[ \begin{gathered}2m + 1 < - 3 \hfill \\ 2m + 1 > 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m < - 2 \hfill \\ m > 1 \hfill \\ \end{gathered} \right.$ .
Câu 17 :
Số mặt phẳng đối xứng của mặt cầu là:
Đáp án : D Lời giải chi tiết :
Mọi mặt phẳng đi qua tâm của mặt cầu đều là mặt phẳng đối xứng của mặt cầu. Vậy có vô số mặt phẳng đối xứng.
Câu 18 :
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:  Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
Đáp án : B Phương pháp giải :
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số và đối chiếu với các đáp án bài cho. Lời giải chi tiết :
Nhận xét: Đồ thị hàm số \(y = f\left( x \right)\) có $\left\{ \begin{align}& \xrightarrow{TCD}x=-\dfrac{3}{2} \\ & \xrightarrow{TCN}y=\dfrac{1}{2} \\ \end{align} \right.$ Vậy hàm số đó là \(y = \dfrac{{x + 2}}{{2x + 3}}\).
Câu 19 :
Tính giá trị của biểu thức \({3^2}{.5^{2 + 2\sqrt 2 }}:{25^{\left( {1 + \sqrt 2 } \right)}}\) có kết quả là:
Đáp án : C Phương pháp giải :
Sử dụng các công thức \(\sqrt[m]{{{a^n}}} = {a^{\dfrac{m}{n}}},\,\,{a^m}.{a^n} = {a^{m + n}}\). Lời giải chi tiết :
\(\begin{array}{l}\,\,\,\,{3^2}{.5^{2 + 2\sqrt 2 }}:{25^{\left( {1 + \sqrt 2 } \right)}}\\ = {3^2}{.5^{2 + 2\sqrt 2 }}:{5^{2 + 2\sqrt 2 }}\\ = {3^2}\\ = 9\end{array}\)
Câu 20 :
Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
Đáp án : C Phương pháp giải :
Sử dụng tỉ số thể tích để tính \({V_{SABM}}\). Áp dụng công thức tính thể tích để suy ra \({d_{M;\left( {SAB} \right)}}\) Lời giải chi tiết :
Vì M là trung điểm của SD nên \(\frac{{{V_{SABM}}}}{{{V_{SABD}}}} = \frac{{SM}}{{SD}} = \frac{1}{2}\) Mà \(\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{1}{2} \Rightarrow {V_{SABD}} = \frac{1}{2}.4{a^3} = 2{a^3}\) \( \Rightarrow {V_{SABM}} = {a^3} = \frac{1}{3}.d\left( {M;\left( {SAB} \right)} \right).{S_{SAB}} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \frac{{3{a^3}}}{{{a^2}}} = 3a\)
Câu 21 :
Cho $n \in Z, n>0$, với điều kiện nào của $a$ thì đẳng thức sau xảy ra: ${a^{ - n}} = \dfrac{1}{{{a^n}}}$?
Đáp án : C Lời giải chi tiết :
Với $a \ne 0, n\in Z, n>0$ thì ${a^{ - n}} = \dfrac{1}{{{a^n}}}$.
Câu 22 :
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Đáp án : D Phương pháp giải :
- Tính diện tích đáy \({S_{A'B'C'D'}}\) và độ dài đường cao \(BB'\). - Tính thể tích khối lăng trụ theo công thức \(V = Sh\). Lời giải chi tiết :
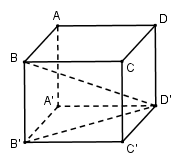 Vì $A'B'C'D'$ là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \) \(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}} = \sqrt {6{a^2} - 2{a^2}} = 2a\) Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)
Câu 23 :
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
Đáp án : A Phương pháp giải :
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\) - Bước 2: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\). Lời giải chi tiết :
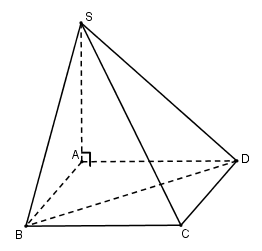 Ta có: \({S_{\Delta BCD}} = \dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{2}{a^2}\) \({V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a.\dfrac{1}{2}{a^2} = \dfrac{{{a^3}}}{6}\)
Câu 24 :
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
Đáp án : A Lời giải chi tiết :
Hai tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.
Câu 25 :
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
Đáp án : D Phương pháp giải :
- Xét phương trình hoành độ giao điểm của hai đồ thị hàm số. - Nêu mối quan hệ giữa số nghiệm của phương trình và số giao điểm. - Giải phương trình tìm nghiệm và suy ra đáp số. Lời giải chi tiết :
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình: $\begin{gathered}{x^3} + 2{x^2} - x + 1 = {x^2} - x + 3 \Leftrightarrow {x^3} + {x^2} - 2 = 0 \hfill \\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 2x + 2} \right) = 0 \Leftrightarrow x = 1 \hfill \\ \end{gathered} $ Như vậy hai đồ thị có $1 $ điểm chung.
Câu 26 :
Công thức nào sau đây là công thức tăng trưởng mũ?
Đáp án : A Lời giải chi tiết :
Công thức lãi kép (hoặc công thức tăng trưởng mũ): \(T = A.{e^{Nr}}\), ở đó \(A\) là số tiền gửi ban đầu, \(r\) là lãi suất, \(N\) là số kì hạn.
Câu 27 :
Trong các hình dưới đây, hình nào là khối đa diện? 
Đáp án : A Phương pháp giải :
Sử dụng tính chất khối đa diện: mối cạnh là cạnh chung của đúng hai mặt. Lời giải chi tiết :
Trong các hình đã cho chỉ có hình a) là khối đa diện. Hình b) có 3 cạnh ở trên không phải cạnh chung của 2 mặt, hình c) và d) có 1 cạnh là không là cạnh chung của 2 mặt.
Câu 28 :
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai? 
Đáp án : D Phương pháp giải :
Quan sát bảng biến thiên và tìm các đường tiệm cận của đồ thị hàm số, các khoảng đồng biến, nghịch biến của hàm số. Lời giải chi tiết :
A đúng vì đồ thị hàm số có đường tiệm cận đứng là \(x = 1\) B đúng vì hàm số luôn đồng biến nên không có cực trị C đúng vì đồ thị hàm số có đường tiệm cận ngang \(y = 2\) D sai vì hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) chứ không đồng biến trên toàn bộ tập số thực \(\mathbb{R}\)
Câu 29 :
Hàm số nào sau đây có đồ thị như hình vẽ? 
Đáp án : D Phương pháp giải :
Quan sát đồ thị hàm số và nhận xét dáng điệu đồ thị, điểm cực đại, cực tiểu, đối chiếu các đáp án đã cho. Lời giải chi tiết :
Từ dáng đồ thị ta có $a > 0$ nên loại A, C Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$ Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$ Kiểm tra ta chỉ thấy đáp án D là phù hợp. Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Câu 30 :
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
Đáp án : D Phương pháp giải :
Sử dụng các công thức logrit của tích, thương: ${\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\left( {0 < a \ne 1;b,c > 0} \right)$ ${\log _a}\left( {\frac{b}{c}} \right) = {\log _a}b - {\log _a}c\left( {0 < a \ne 1;b,c > 0} \right)$ Lời giải chi tiết :
Ta có: ${\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\left( {0 < a \ne 1;b,c > 0} \right)$ ${\log _a}\left( {\dfrac{b}{c}} \right) = {\log _a}b - {\log _a}c\left( {0 < a \ne 1;b,c > 0} \right)$
Câu 31 :
Cho hàm số: $f(x) = - 2{x^3} + 3{x^2} + 12x - 5.$ Trong các mệnh đề sau, tìm mệnh đề sai?
Đáp án : D Phương pháp giải :
Phương pháp xét tính đơn điệu của hàm số. - Bước 1: Tìm TXĐ của hàm số. - Bước 2: Tính đạo hàm $f'\left( x \right)$, tìm các điểm ${x_1},{x_2},...,{x_n}$ mà tại đó đạo hàm bằng $0$ hoặc không xác định. - Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số. + Các khoảng mà $f'\left( x \right) > 0$ là các khoảng đồng biến của hàm số. + Các khoảng mà $f'\left( x \right) < 0$ là các khoảng nghịch biến của hàm số. Lời giải chi tiết :
$f\left( x \right) = - 2{x^3} + 3{x^2} + 12x - 5 \Rightarrow f'\left( x \right) = - 6{x^2} + 6x + 12 = 0 \Leftrightarrow x = 2;x = - 1$ Ta có: $y' < 0,\forall x \in \left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 1} \right);\left( {2; + \infty } \right)$ và $y' > 0,\forall x \in \left( { - 1 ; 2} \right)$ nên nó đồng biến trên khoảng $\left( { - 1;2} \right)$. Đối chiếu với các đáp án đã cho ta thấy các Đáp án A, B, C đều đúng vì các khoảng đó đều là khoảng nằm trong khoảng nghịch biến hoặc đồng biến của hàm số, chỉ có đáp án D sai.
Câu 32 :
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Đáp án : A Phương pháp giải :
- Xác định tọa độ 2 điểm cực trị $A,\;B.$ - Tính diện tích tam giác $OAB$ theo công thức: $S = \dfrac{1}{2}a.h$ (với $a$ là độ dài đáy, $h$ là độ dài đường cao tương ứng với đáy đã chọn). Lời giải chi tiết :
 $\begin{array}{*{20}{l}}{y = {x^3} - 3x + 2 \Rightarrow y' = 3{x^2} - 3}\\{y' = 0 \Leftrightarrow x = {\rm{\;}} \pm 1}\end{array}$ Tọa độ $2$ điểm cực trị : $A(1;{\mkern 1mu} 0),{\mkern 1mu} {\mkern 1mu} B( - 1;4)$ Khi đó ${S_{\Delta OAB}} = \dfrac{1}{2}.OA.{d(B,OA)} = \dfrac{1}{2}.\left| {{x_A}} \right|.\left| {{y_B}} \right| = \dfrac{1}{2}.\left| 1 \right|.\left| 4 \right| = 2$
Câu 33 :
Cho hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.$ Tìm $m$ để đồ thị hàm số có hai điểm cực trị là $A, B$ sao cho đường thẳng $AB$ vuông góc với $d:\,x - y - 9 = 0$
Đáp án : C Phương pháp giải :
- Bước 1: Tính $y'$. - Bước 2: Lấy $y$ chia $y'$ ta được đa thức dư $g\left( x \right) = mx + n$ là đường thẳng đi qua hai cực trị. - Bước 3: Đường thẳng $d$ vuông góc $d' \Leftrightarrow {k_d}.{k_{d'}} = - 1$. Lời giải chi tiết :
$y' = 6{x^2} - 6\left( {m + 1} \right)x + 6m$ Đồ thị hàm số có hai điểm cực trị \(A,B\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = 9{\left( {m + 1} \right)^2} - 36m > 0\) \( \Leftrightarrow 9{m^2} - 18m + 9 > 0\) \( \Leftrightarrow 9{\left( {m - 1} \right)^2} > 0\) \( \Leftrightarrow m \ne 1\) Khi đó, $y = y'.\left( \dfrac{1}{3}x -\dfrac{{m + 1}}{6} \right) + \left[ {4m - {{\left( {m + 1} \right)}^2}} \right]x + m\left( {m + 1} \right)$ Đường thẳng \(AB:\) \(y = \left[ {4m - {{\left( {m + 1} \right)}^2}} \right]x + m\left( {m + 1} \right)\) có hệ số góc $k={4m - {{\left( {m + 1} \right)}^2}}$ Đường thẳng \(d:\,y = x - 9\) có hệ số góc $k=1$ \(\begin{array}{l}AB \bot d\\ \Leftrightarrow \left[ {4m - {{\left( {m + 1} \right)}^2}} \right].1 = - 1\\ \Leftrightarrow 4m - {m^2} - 2m - 1 = - 1\\ \Leftrightarrow - {m^2} + 2m = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\end{array}\)
Câu 34 :
Đồ thị hàm số $y = \dfrac{{x - 3}}{{{x^2} + x - 2}}$ có bao nhiêu đường tiệm cận đứng?
Đáp án : C Phương pháp giải :
Đường thẳng $x = {x_0}$ là tiệm cận đứng của đồ thị hàm phân thức $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ nếu ${x_0}$ là nghiệm của đa thức $g\left( x \right)$ nhưng không phải nghiệm của đa thức $f\left( x \right)$ Lời giải chi tiết :
Dễ thấy đa thức dưới mẫu có hai nghiệm $x = 1$ và $x = - 2$ và hai nghiệm này đều không phải nghiệm của tử thức. $ \Rightarrow $ Đồ thị hàm số đã cho có $2$ tiệm cận đứng.
Câu 35 :
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng: 
Đáp án : D Phương pháp giải :
- Dựa vào dấu \(f'\left( x \right)\) xác định GTLN của hàm số \(y = f\left( x \right)\) trên \(\left[ {1;2} \right]\). - Dựa vào TXĐ của hàm số \(y = f'\left( x \right)\) và điểm đi qua \(\left( {0; - 3} \right)\), biểu diễn 3 trong 4 ẩn \(a,\,\,b,\,\,c,\,\,d\) theo ẩn còn lại. - Tính \(f\left( { - 2} \right)\). Lời giải chi tiết :
Dựa vào đồ thị hàm số ta thấy \(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\), do đó \(f'\left( x \right) < 0\,\,\forall x \in \left( {1;2} \right)\). \( \Rightarrow \) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {1;2} \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {1;2} \right]} f\left( x \right) = f\left( 2 \right)\)\( \Rightarrow \frac{{2a + b}}{{2c + d}} = 3\). Ta có: \(f'\left( x \right) = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ { - 1} \right\} \Rightarrow \) \( - c + d = 0 \Leftrightarrow c = d\). Đồ thị hàm số \(y = f'\left( x \right)\) đi qua điểm \(\left( {0; - 3} \right)\) \( \Rightarrow \frac{{ad - bc}}{{{d^2}}} = - 3\). \( \Rightarrow \frac{{ad - bd}}{{{d^2}}} = - 3 \Leftrightarrow a - b = - 3d = - 3c\). Lại có \(\frac{{2a + b}}{{2c + d}} = 3 \Leftrightarrow \frac{{2a + b}}{{2c + c}} = 3\) \( \Leftrightarrow 2a + b = 9c\). Ta có: \(\left\{ \begin{array}{l}a - b = - 3c\\2a + b = 9c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2c\\b = 5c\end{array} \right.\)\( \Rightarrow y = \frac{{2cx + 5c}}{{cx + c}}\). Vậy \(y\left( { - 2} \right) = \frac{{ - 4c + 5c}}{{ - 2c + c}} = - 1\).
Câu 36 :
Cho hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có bảng biến thiên:  Giá trị của ${c^2} - {d^2}$ bằng:
Đáp án : B Phương pháp giải :
- Quan sát bảng biến thiên, tìm các đường tiệm cận đứng, ngang của đồ thị hàm số. - Tìm $c,d \Rightarrow {c^2} - {d^2}$ Lời giải chi tiết :
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có $\left\{ \begin{gathered} \xrightarrow{{TCD}}x = - \dfrac{d}{c} = - 1 \hfill \\ \xrightarrow{{TCN}}y = \dfrac{2}{c} = 2 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} c = 1 \hfill \\ d = 1 \hfill \\ \end{gathered} \right. \Rightarrow {c^2} - {d^2} = {1^2} - {1^2} = 0$
Câu 37 :
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Đáp án : A Phương pháp giải :
- Nêu mối quan hệ giữa số nghiệm của phương trình và số giao điểm của $d$ và $\left( C \right)$. - Khảo sát hàm số $y = {x^5} + {x^3} - \sqrt {1 - x} $ trên $\left( { - \infty ;1} \right]$ và từ đó suy ra điều kiện của $m$. Lời giải chi tiết :
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ và đường thẳng d: $y = - m$. Xét hàm số (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ có: $y' = 5{x^4} + 3{x^2} + \dfrac{1}{{2\sqrt {1 - x} }} > 0\,\,\forall x \in \left( { - \infty ;1} \right)$$ \Rightarrow $ hàm số luôn đồng biến trên $\left( { - \infty ;1} \right]$. Lại có $y\left( 1 \right) = 2$. Ta có BBT: 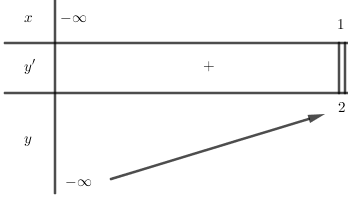 Theo BBT ta thấy pt có nghiệm $ \Leftrightarrow - m \leqslant 2 \Leftrightarrow m \geqslant - 2$.
Câu 38 :
Tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^3}}}{3} - 2{x^2} + x + 2$ song song với đường thẳng $y = - 2x + 5$ có phương trình là:
Đáp án : A Phương pháp giải :
Tiếp tuyến song song với đường thẳng $y = - 2x + 5$ thì có hệ số góc bằng với hệ số góc của đường thẳng nên $y' = - 2$. Giải phương trình $y' = - 2$ tìm các nghiệm rồi suy ra tọa độ tiếp điểm, từ đó viết được phương trình tiếp tuyến. Đường thẳng $d$ đi qua $A\left( {{x_0};{y_0}} \right)$ và có hệ số góc $k$ có phương trình $y = k\left( {x - {x_0}} \right) + {y_0}$ Lời giải chi tiết :
Tiếp tuyến $(d)$ song song với đường thẳng $y = - 2x + 5$ nên có hệ số góc . Suy ra $y' = - 2$ hay ${x^2} - 4x + 1 = - 2 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0$ $ \Rightarrow \left[ \begin{gathered}x = 1,y = \dfrac{4}{3} \hfill \\x = 3,y = - 4 \hfill \\ \end{gathered} \right.$ Với $x = 1;y = \dfrac{4}{3}$ thì ${d_1}:y = - 2\left( {x - 1} \right) + \dfrac{4}{3}$ hay ${d_1}:y = - 2x + \dfrac{{10}}{3}$ Với $x = 3;y = - 4$ thì ${d_2}:y = - 2\left( {x - 3} \right) - 4$ hay ${d_2}:y = - 2x + 2$
Câu 39 :
Số \(9465779232\) có bao nhiêu ước số nguyên dương?
Đáp án : B Phương pháp giải :
Phân tích số đã cho ra thừa số nguyên tố: \(M = {x^m}.{y^n}.{z^t}\) thì \(M\) có \(\left( {m + 1} \right)\left( {n + 1} \right)\left( {t + 1} \right)\) ước nguyên dương. Lời giải chi tiết :
Ta có: \(9465779232 = {2^5}{.3^6}{.7^4}{.13^2}\) Như vậy số đã cho có số ước nguyên dương là: \(\left( {5 + 1} \right)\left( {6 + 1} \right)\left( {4 + 1} \right)\left( {2 + 1} \right) = 630\) ước.
Câu 40 :
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Đáp án : B Phương pháp giải :
Lần lượt áp dụng các công thức: ${\log _a}xy = {\log _a}x + {\log _a}y$ ${\log _a}{b^n} = n{\log _a}b$ ${\log _a}a = 1$ Lời giải chi tiết :
Ta có: $\log_a{a^2}{b^4} = \log_a{a^2} + \log_a{b^4} $ $= 2\log_a a + 4\log_a b = 2 + 4p$
Câu 41 :
Cho các phát biểu sau: (I). Nếu \(C = \sqrt {AB} \) thì \(2\ln C = \ln A + \ln B\) với $A, B$ là các biểu thức luôn nhận giá trị dương. (II). \(\left( {a - 1} \right){\log _a}x \ge 0 \Leftrightarrow x \ge 1\) với \(a > 0,a \ne 1\) (III). \({m^{{{\log }_a}m}} = {n^{{{\log }_a}n}},\) với \(m,n > 0\) và \(a > 0,a \ne 1\) (IV).\(\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty \) Số phát biểu đúng là
Đáp án : C Lời giải chi tiết :
Ta có ${C^2} = AB \Rightarrow {{\mathop{\rm lnC}\nolimits} ^2} = {\mathop{\rm \ln (AB)}\nolimits} \Rightarrow 2\ln C = \ln A + \ln B$ nên I đúng Ta có $\left( {a - 1} \right){\log _a}x \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a - 1 > 0}\\{{{\log }_a}x \ge 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{a - 1 < 0}\\{{{\log }_a}x \le 0}\end{array}} \right.}\end{array}} \right. $ $\Leftrightarrow x\ge 1$ suy ra II đúng. Logarit cơ số $m$ hai vế ta được ${\log _a}m.{\log _m}m \ne {\log _a}n.{\log _m}n$ suy ra III sai Ta có $\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty $ đúng nên IV đúng. Vậy có \(3\) phát biểu đúng.
Câu 42 :
Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\).
Đáp án : D Phương pháp giải :
Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định nếu \(x > 0\). Lời giải chi tiết :
Điều kiện : \(\dfrac{{ - 3}}{{2 - 2x}} > 0 \Leftrightarrow 2 - 2x < 0 \Leftrightarrow x > 1.\)
Câu 43 :
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng
Đáp án : A Phương pháp giải :
Sử dụng công thức tính tỉ số thể tích hai khối chóp tam giác: \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\) Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao. Lời giải chi tiết :
Gọi D là giao điểm của MB và EN thì D là trung điểm của MB. Ta có: \({V_{MNEF}} = {V_{M.NEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {M,\left( {NEF} \right)} \right)\) Do D là trung điểm của MB và MB cắt (EFN) tại D nên \(d\left( {M,\left( {NEF} \right)} \right) = d\left( {B,\left( {NEF} \right)} \right)\) \( \Rightarrow {V_{MNEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {B,\left( {NEF} \right)} \right)\)\( = {V_{B.NEF}}\) Mà \(\dfrac{{{V_{B.NEF}}}}{{{V_{B.CAS}}}} = \dfrac{{BN}}{{BC}}.\dfrac{{BE}}{{BA}}.\dfrac{{BF}}{{BS}}\)\( = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{6}\) \( \Rightarrow {V_{B.NEF}} = \dfrac{1}{6}{V_{B.CAS}} = \dfrac{1}{6}{V_{S.ABC}}\) Vì SA=SB=SC nên \(S\) nằm trên trục đường tròn ngoại tiếp tam giác ABC. Mà ABC vuông cân nên M là tâm đường tròn ngoại tiếp tam giác. Do đó \(SM \bot \left( {ABC} \right)\). Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.4.4 = 8\) Tam giác ABC vuông cân tại B nên \(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} \\ = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \\ \Rightarrow AM = \dfrac{1}{2}AC = \dfrac{1}{2}.4\sqrt 2 = 2\sqrt 2 \end{array}\) Tam giác \(SMA\) vuông tại M nên theo Pitago ta có: \(SM = \sqrt {S{A^2} - A{M^2}} \)\( = \sqrt {{{12}^2} - {{\left( {2\sqrt 2 } \right)}^2}} = 2\sqrt {34} \) Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SM\)\( = \dfrac{1}{3}.8.2\sqrt {34} \) $ = \dfrac{{16\sqrt {34} }}{3}$ Thể tích khối tứ diện MNEF là: \({V_{MNEF}} = \dfrac{1}{6}.{V_{S.ABC}}\)\( = \dfrac{1}{6}.\dfrac{{16\sqrt {34} }}{3} = \dfrac{{8\sqrt {34} }}{9}\)
Câu 44 :
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy $ABCD$ là hình chữ nhật với \(AB = \sqrt 3 ,AD = \sqrt 7 \). Hai mặt bên $\left( {ABB'A'} \right)$ và $\left( {ADD'A'} \right)$ lần lượt tạo với đáy những góc \({45^0}\) và \({60^0}\). Tính thể tích khối hộp nếu biết cạnh bên bằng $1$.
Đáp án : A Phương pháp giải :
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng nằm trong các mặt phẳng mà cùng vuông góc với giao tuyến. - Tính độ dài đường cao và diện tích đáy lăng trụ. - Tính thể tích lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao. Lời giải chi tiết :
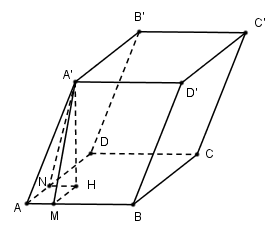 Kẻ \(A'H \bot \left( {ABCD} \right);HM \bot AB;HN \bot AD\) Ta có: \(\left. \begin{array}{l}A'H \bot AB\\HM \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {A'HM} \right) \Rightarrow AB \bot A'M\) \(\left. \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABB'A'} \right) \supset A'M \bot AB\\\left( {ABCD} \right) \supset HM \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {A'M;HM} \right)} = \widehat {A'MH} = {45^o}\) Chứng minh tương tự ta có \(\widehat {A'NH} = {60^0}\) Đặt \(A'H = x\) khi đó ta có: \(A'N = \dfrac{x}{{\sin 60}} = \dfrac{{2x}}{{\sqrt 3 }},AN = \sqrt {AA{'^2} - A'{N^2}} = \sqrt {1 - \dfrac{{4{x^2}}}{3}} = HM\) Mà \(HM = x.\cot 45 = x\) $ \Rightarrow x = \sqrt {1 - \dfrac{{4{x^2}}}{3}} \Leftrightarrow {x^2} = 1 - \dfrac{{4{x^2}}}{3} \Leftrightarrow \dfrac{{7{x^2}}}{3} = 1 \Rightarrow {x^2} = \dfrac{3}{7} \Rightarrow x = \sqrt {\dfrac{3}{7}} $ \({S_{ABCD}} = \sqrt 3 .\sqrt 7 = \sqrt {21} \) Vậy \({V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = \sqrt {\dfrac{3}{7}} .\sqrt {21} = 3\)
Câu 45 :
Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
Đáp án : B Lời giải chi tiết :
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\). Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\). Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\). Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\). \( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\). Thể tích khối chóp \(S.ABC\) là: \(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\) Áp dụng bất đẳng thức Cô-si ta có: \(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\) Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\). \( \Rightarrow a = 3,\,\,b = 2\). Vậy \(a + b = 3 + 2 = 5\).
Câu 46 :
Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
Đáp án : A Phương pháp giải :
- Tính số tiền bà Hoa rút ra sau 5 năm theo công thức $T = A{\left( {1 + r} \right)^N}$. - Tính số tiền lãi lần đầu. - Tính số tiền bà đem gửi lần 2. - Tính số tiền sau 5 năm lần 2 theo công thức: $T = A{\left( {1 + r} \right)^N}$ - Tính số tiền lãi lần 2 và suy ra đáp số. Lời giải chi tiết :
Số tiền bà Hoa rút sau 5 năm đầu là: $100{\left( {1 + 8\% } \right)^5} = 146,932$ triệu. Số tiền lãi lần 1 là: $146,932 - 100 = 46,932$ triệu. Số tiền bà gửi tiếp vào ngân hàng là: $146,932:2 = 73,466$ triệu Số tiền và có sau 5 năm là: $73,466{\left( {1 + 8\% } \right)^5} = 107,946$ triệu. Số tiền lãi lần 2 là: $107,946 - 73,466 = 34,480$ triệu. Tổng số tiền lãi sau 2 lần là: $46,932 + 34,480 = 81,412$ triệu.
Câu 47 :
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?
Đáp án : B Lời giải chi tiết :
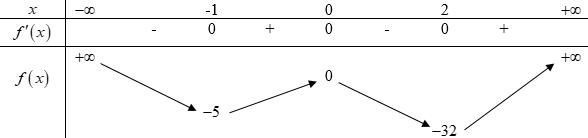
Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) ta có \(\begin{array}{l}f'\left( x \right) = 12{x^3} - 12{x^2} - 24x\\f'\left( x \right) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\end{array}\) BBT:
Ta có đồ thị \(y = f\left( x \right)\,\,\left( C \right)\) như sau:
Để \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị thì: TH1: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 2 điểm phân biệt khác cực trị \( \Leftrightarrow \left[ \begin{array}{l} - m > 0\\ - 32 < - m < - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\5 < m < 32\end{array} \right.\) Mà \(m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\) : 26 giá trị. TH2: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 3 điểm phân biệt, trong đó có 1 cực trị \( \Leftrightarrow \left[ \begin{array}{l} - m = 0\\ - m = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,(L)\\m = 5\,(TM)\end{array} \right.\) Vậy, có tất cả 27 giá trị của m thỏa mãn.
Câu 48 :
Cho hàm số \(y = \dfrac{x}{{1 - x}}\,\,\left( C \right)\) và điểm \(A\left( { - 1;1} \right)\). Tìm \(m\) để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) sao cho \(A{M^2} + A{N^2}\) đạt giá trị nhỏ nhất.
Đáp án : A Phương pháp giải :
- Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình hoành độ giao điểm có hai nghiệm phân biệt. - Áp dụng định lí Vi-ét. - Sử dụng công thức độ dài đường trung tuyến \(A{I^2} = \dfrac{{A{M^2} + A{N^2}}}{2} - \dfrac{{M{N^2}}}{4}\) (với \(I\) là trung điểm của \(MN\)), từ đó rút \(A{M^2} + A{N^2}\) theo \(m\). - Sử dụng phương pháp hàm số để tìm GTNN của hàm số. Lời giải chi tiết :
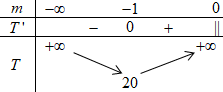
Xét phương trình hoành độ giao điểm:. \(\begin{array}{l}\,\,\,\,\,\,\dfrac{x}{{1 - x}} = mx - m - 1\,\,\left( {x \ne 1} \right)\\ \Leftrightarrow x = \left( {mx - m - 1} \right)\left( {1 - x} \right)\\ \Leftrightarrow x = mx - m - 1 - m{x^2} + mx + x\\ \Leftrightarrow m{x^2} - 2mx + m + 1 = 0\,\,\,\left( * \right)\end{array}\) Để đường thẳng \(d:\,\,y = mx - m - 1\) cắt \(\left( C \right)\) tại 2 điểm phân biệt \(M,\,\,N\) thì phương trình (*) phải có 2 nghiệm phân biệt khác \(1\) \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {m^2} - m\left( {m + 1} \right) > 0\\m - 2m + m + 1 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - m > 0\\1 \ne 0\end{array} \right. \Leftrightarrow m < 0\). Khi đó hoành độ của hai điểm \(M,\,\,N\) là nghiệm của phương trình (*), áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_M} + {x_N} = 2\\{x_M}.{x_N} = \dfrac{{m + 1}}{m}\end{array} \right.\). Ta có: \(\left\{ \begin{array}{l}{y_M} = m{x_M} - m - 1\\{y_N} = m{x_N} - m - 1\end{array} \right.\) \( \Rightarrow {y_M} + {y_N} = \left( {{x_M} + {x_N}} \right) - 2m - 2 = - 2\). Gọi \(I\) là trung điểm của \(MN\), ta có \(I\left( {1; - 1} \right)\) \( \Rightarrow A{I^2} = {2^2} + {\left( { - 2} \right)^2} = 8\). \(\begin{array}{l}M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {m{x_M} - m - 1 - m{x_N} + m + 1} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{x_M} - {x_N}} \right)^2} + {m^2}{\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right){\left( {{x_M} - {x_N}} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = \left( {1 + {m^2}} \right)\left[ {4 - 4\dfrac{{m + 1}}{m}} \right]\\\,\,\,\,\,\,\,\,\,\,\,\, = - 4\dfrac{{1 + {m^2}}}{m}\end{array}\) Do \(M{N^2} > 0\) nên \(m < 0\). Đặt \(T = A{M^2} + A{N^2}\) Ta có: \(\begin{array}{l}A{I^2} = \dfrac{{A{M^2} + A{N^2}}}{2} - \dfrac{{M{N^2}}}{4}\\ \Rightarrow 4A{I^2} = 2T - M{N^2}\\ \Leftrightarrow T = \dfrac{{4A{I^2} + M{N^2}}}{2} \Leftrightarrow T = \dfrac{{4.8 - 4\dfrac{{1 + {m^2}}}{m}}}{2}\\ \Leftrightarrow T = 16 - 2\dfrac{{1 + {m^2}}}{m} \Leftrightarrow T = \dfrac{{ - 2{m^2} + 16m - 2}}{m}\end{array}\) Ta có: \(\begin{array}{l}T' = \dfrac{{\left( { - 4m + 16} \right)m - \left( { - 2{m^2} + 16m - 2} \right)}}{{{m^2}}}\\T' = \dfrac{{ - 4{m^2} + 16m + 2{m^2} - 16m + 2}}{{{m^2}}}\\T' = \dfrac{{ - 2{m^2} + 2}}{{{m^2}}} = 0 \Leftrightarrow m = \pm 1\end{array}\) BBT:
Từ BBT ta thấy \(\min T = 20 \Leftrightarrow m = - 1\) .
Câu 49 :
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên  Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
Đáp án : B Phương pháp giải :
- Biến đổi bất phương trình về dạng \(g(x)>m\). - Xét hàm \(y=g(x)\) và tìm GTNN của \(g(x)\). - Bài toán thỏa khi \(m<\mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\) Lời giải chi tiết :
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\). Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau: 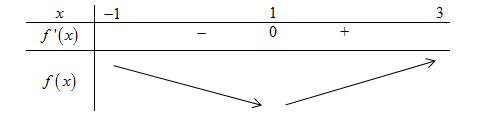 Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\). \(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\) \( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\). Vậy \(m < f\left( 1 \right) - 1\).
Câu 50 :
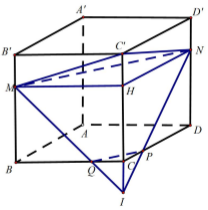
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).
Đáp án : B Lời giải chi tiết :
Gọi cạnh của hình lập phương là \(a\). Ta có: \(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\). \(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {BCC'B'} \right)\) kẻ \(MQ\parallel B'C\,\,\left( {Q \in BC} \right)\). \(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\). \(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {ABCD} \right)\) kẻ \(PQ\parallel BD\,\,\left( {P \in DC} \right)\). Khi đó \(\left( \alpha \right) \equiv \left( {MNPQ} \right)\). Theo cách dựng ta có \(BQ = 2QC,\,\,DP = 2PC,\,\,DN = 2ND'\). Gọi \(H\) là điểm thuộc \(CC'\) sao cho \(CH = 2HC'\). Khi đó ta có: \({V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}}\). Xét hình chóp \(C'.MHN\) có \(C'H = \dfrac{a}{3}\), \({S_{\Delta MHN}} = \dfrac{1}{2}{a^2}\). \( \Rightarrow {V_{C'.MHN}} = \dfrac{1}{3}C'H.{S_{\Delta MHN}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{{18}} = \dfrac{V}{{18}}\). Xét hình chóp cụt \(CQP.MHN\) có \(\begin{array}{l}{V_{CQP.MHN}} = {V_{I.MHN}} - {V_{I.CQP}} = \dfrac{1}{3}\left( {IH.{S_{\Delta MHN}} - IC.{S_{\Delta CQP}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}\left( {a.\dfrac{1}{2}{a^2} - \dfrac{a}{3}.\dfrac{1}{2}.\dfrac{a}{3}.\dfrac{a}{3}} \right) = \dfrac{{13{a^3}}}{8} = \dfrac{{13V}}{{81}}\end{array}\) \( \Rightarrow {V_1} = {V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}} = \dfrac{V}{{18}} + \dfrac{{13V}}{{81}} = \dfrac{{35V}}{{162}}\). Vậy \(\dfrac{{{V_1}}}{V} = \dfrac{{35}}{{162}}\) |