Đề kiểm tra 45 phút chương 3 phần Đại số 9 - Đề số 2

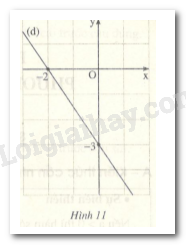
Đề bài

I-Phần trắc nghiệm khách quan

Hãy chọn đáp án đúng:

Câu 1 (0,5 điểm): Một hệ phương trình bậc nhất hai ẩn:

(A) Luôn có một nghiệm duy nhất

(B) Luôn có vô số nghiệm

(C) Có thể có nghiệm duy nhất

(D) Không thể có vô số nghiệm

Câu 2 (0,5 điểm): Phương trình bậc nhất hai ẩn 2x + 0y = 6 có tập nghiệm là: 

(A) \(S = \left\{ 3 \right\}\)                              (B) \(S = \left\{ {\left( {3\,\,;\,\,0} \right)} \right\}\)

(C) \(S = \left\{ {\left( {x\,\,;\,\,3} \right)\left| {x \in R} \right.} \right\}\)       (D) \(S = \left\{ {\left( {3\,\,;\,\,y} \right)\left| {y \in R} \right.} \right\}\)

Câu 3 (0,5 điểm): Hai cặp số (-1 ; 1) và (-1 ; -2) là hai nghệm của một phương trình bậc nhất hai ẩn. Tập nghiệm của phương trình đó là:

(A) \(S = \left\{ {\left( {x\,\,;\,\,1} \right)\left| {x \in R} \right.} \right\}\)                   (B) \(S = \left\{ {\left( { - 1\,\,;\,\,y} \right)\left| {y \in R} \right.} \right\}\)

(C) \(S = \left\{ {\left( {x\,\,;\,\, - 2} \right)\left| {x \in R} \right.} \right\}\)                (D) \(S = \left\{ {\left( { - 1\,\,;\,\,1} \right);\left( { - 1\,\,;\,\, - 2} \right)} \right\}\)

Câu 4 (0,5 điểm): Một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 2\\\left( {2 - \sqrt 5 } \right)x + \left( {1 - \sqrt 5 } \right)y = 2\end{array} \right.\) là:

(A) (0 ; 1)                                (B) (-2 ; 4)

(C) (2; -2)                                (D) (-4 ; 5)

Câu 5 (0,5 điểm): Cho hai hệ phương trình \((I)\,\,\left\{ \begin{array}{l}2x - y = 5\\2y - x = 5\end{array} \right.\)  và \((II)\,\,\left\{ \begin{array}{l}x = y + 1\\y = x + 1\end{array} \right.\)

Khi đó:

(A) Hệ (I) có một nghiệm duy nhất và hệ (II) có một nghiệm duy nhất.

(B) Hệ (I) có vô số nghiệm và hệ (II) có một nghiệm duy nhất.

(C) Hệ (I) có một nghiệm duy nhất và hệ (II) vô nghiệm.

(D) Hệ (I) có vô số nghiệm và hệ (II)  vô  nghiệm

Câu 6 (0,5 điểm): Đường thẳng (d) trong hình 11 biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn sau:

(A) -2x – 3y – 6 = 0

(B) 2y – 3x + 6 = 0

(C) 2y – 3x - 6 = 0

(D) -2y + 3x + 6 = 0

(II) Phần tự luận

Câu 7 (4 điểm): Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}3x - y = 1\\2x - y = 3\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x - 2y = 6\\\dfrac{1}{{\sqrt 2 }}x - y\sqrt 2  = 3\sqrt 2 \end{array} \right.\)

Câu 8 (3 điểm): Một chuyển động đi từ A đến B với vận tốc 50m/ph rồi đi tiếp từ B đến C với vận tốc 45m/ph. Tổng cộng, vật đó đi được quãng đường dài 165 m. Tính thời gian đi trên mỗi đoạn đường AB và BC, biết rằng thời gian vật đi trên đoạn AB ít hơn thời gian vật đi trên đoanh đường BC là 30 giây.

Lời giải chi tiết

I-Phần trắc nghiệm khách quan

 Câu 1: C     Câu 2: D      Câu 3: B 

Câu 4: C     Câu 5: C      Câu 6:  A

Câu 1: Chọn C

Phương pháp

Sử dụng kiến thức về nghiệm của hệ phương trình bậc nhất hai ẩn (có thẻ có 1 nghiệm, vô nghiệm hoặc vô số nghiệm)

Lời giải

Hệ phương trình bậc nhất hai ẩn có thể vô nghiệm, vô số nghiệm hoặc có nghiệm duy nhất.

Câu 2: Chọn D

Phương pháp

Xét phương trình bậc nhất hai ẩn \({\rm{ax}} + by = c\)

Nếu \(a \ne 0\)  và \(b = 0\)  thì phương trình có nghiệm  \(\left\{ \begin{array}{l}y \in R\\x = \dfrac{c}{a}\end{array} \right.\)

Hay tập nghiệm của phương trình là \(S = \left\{ {\left( {\dfrac{c}{a};y} \right)|y \in \mathbb{R}} \right\}\)

Lời giải

Ta có \(2x + 0y = 6 \Leftrightarrow x = 3\)

Phương trình có tập nghiệm \(S = \left\{ {\left( {3;y} \right)|y \in \mathbb{R}} \right\}\).

Câu 3: Chọn B

Phương pháp

Dựa vào nhận xét: Phương trình bậc nhất hai ẩn luôn có vô số nghiệm

Và phương trình bậc nhất hai ẩn \({\rm{ax}} + by = c\)  có nghiệm  \(\left\{ \begin{array}{l}y \in R\\x = \dfrac{c}{a}\end{array} \right.\) với \(a \ne 0\)  và \(b = 0\).

Khi đó tập nghiệm của phương trình là \(S = \left\{ {\left( {\dfrac{c}{a};y} \right)|y \in \mathbb{R}} \right\}\)

Lời giải

Vì hai cặp số \(\left( { - 1;1} \right)\) và \(\left( { - 1; - 2} \right)\) là hai nghiệm của một phương trình bậc nhất hai ẩn nên các cặp số  \(\left\{ \begin{array}{l}y \in R\\x =  - 1\end{array} \right.\) đều là nghiệm của phương trình đó. Suy ra, tập nghiệm của phương trình này là \(S = \left\{ {\left( { - 1;y} \right)|y \in \mathbb{R}} \right\}\)

Câu 4: Chọn C

Phương pháp

Giải hệ phương trình bằng phương pháp thế

Lời giải

Ta có \(\left\{ \begin{array}{l}3x + 2y = 2\\\left( {2 - \sqrt 5 } \right)x + \left( {1 - \sqrt 5 } \right)y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{2 - 3x}}{2}\\\left( {2 - \sqrt 5 } \right)x + \left( {1 - \sqrt 5 } \right).\dfrac{{2 - 3x}}{2} = 2\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{2 - 3x}}{2}\\\left( {4 - 2\sqrt 5 } \right)x + \left( {1 - \sqrt 5 } \right)\left( {2 - 3x} \right) = 4\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{2 - 3x}}{2}\\\left( {4 - 2\sqrt 5 } \right)x - \left( {3 - 3\sqrt 5 } \right)x + 2 - 2\sqrt 5  = 4\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{2 - 3x}}{2}\\\left( {1 + \sqrt 5 } \right)x = 2 + 2\sqrt 5 \end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y =  - 2\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2; - 2} \right)\).

Chú ý:

Các em có thể thay từng cặp số ở đáp án vào để kiểm tra xem nó có là nghiệm của hệ hay không.

Cặp số \(\left( {{x_0};{y_0}} \right)\) là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\)  khi  \(\left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c'\end{array} \right.\)

Câu 5: Chọn C

Phương pháp

Sử dụng phương pháp thế hoặc cộng đại số giải từng hệ phương trình rồi kết luận

Lời giải

Ta xét hệ (I) \(\left\{ \begin{array}{l}2x - y = 5\\2y - x = 5\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = 2x - 5\\2\left( {2x - 5} \right) - x = 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3x = 15\\y = 2x - 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 5\end{array} \right.\)

Suy ra hệ (I) có nghiệm duy nhất  \(\left( {x;y} \right) = \left( {5;5} \right)\)

Ta xét hệ (II) \(\left\{ \begin{array}{l}x = y + 1\\y = x + 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = y + 1\\y = y + 1 + 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = y + 1\\0 = 2\,\end{array}\,(Vô \,\,nghiệm) \right.\)  

Vậy hệ phương trình (II) vô nghiệm.

Chú ý:

Các em cũng có thể dự đoán số nghiệm của hệ phương trình mà không cần giải hệ.

Tập nghiệm của hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,\\a'x + b'y = c'\,\,\,\end{array} \right.\) được biểu diễn bởi tập hợp các điểm chung của hai đường thẳng \(d:ax + by = c\) và \(d':a'x + b'y = c'.\)

Trường hợp 1. \(d \cap d' = A\left( {{x_0};{y_0}} \right) \Leftrightarrow \) Hệ phương trình có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\);

Trường hợp 2. \(d//d' \Leftrightarrow \) Hệ phương trình vô nghiệm;

Trường hợp 3. \(d \equiv d' \Leftrightarrow \) Hệ phương trình có vô số nghiệm.

Câu 6: Chọn A

Phương pháp

Xác định hai điểm thuộc đồ thị hàm số.

Ta xác định phương trình đường thẳng \(\left( d \right)\,\)

Từ đó sử dụng tập nghiệm của phương trình \({\rm{ax}} + by = c\) được biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)

Lời giải

Từ đồ thị hàm số ta thấy hai điểm có tọa độ \(\left( {0; - 3} \right);\left( { - 2;0} \right)\) thuộc đường thẳng \(\left( d \right).\)

Gọi phương trình đường thẳng \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\)

Thay \(x = 0;y =  - 3\) vào phương trình \(y = ax + b\) ta được \( - 3 = a.0 + b \Rightarrow b =  - 3\)

Thay \(x =  - 2;y = 0\) vào phương trình \(y = ax + b\) ta được \(0 =  - 2a + b\)  mà \(b =  - 3 \Rightarrow  - 2a - 3 = 0 \Leftrightarrow a =  - \dfrac{3}{2}\)(TM )

Vậy  phương trình đường thẳng \(\left( d \right):y =  - \dfrac{3}{2}x - 3\)

Hay đường thẳng \(\left( d \right)\) biểu diễn tập nghiệm của phương trình \(y =  - \dfrac{3}{2}x - 3 \)\(\Leftrightarrow 2y =  - 3x - 6\)\( \Leftrightarrow  - 2y - 3x - 6 = 0\)

Các em có thể làm theo cách sau:

Xác định hai điểm thuộc đồ thị hàm số.

Thay tọa độ hai điểm đó vào mỗi phương trình ở đáp án để xác định xem cặp số đó có là nghiệm hay không.

Cặp số \(\left( {{x_0};{y_0}} \right)\) là một nghiệm của phương trình \(ax + by + c = 0 \Leftrightarrow a{x_0} + b{y_0} + c = 0\)

(II) Phần tự luận

Câu 7 

Phương pháp

Sử dụng phương pháp thế hoặc cộng đại số để giải hệ phương trình

Lời giải

a) \(\left\{ \begin{array}{l}3x - 5y = 1\\2x - y = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = 2x - 3\\3x - 5\left( {2x - 3} \right) = 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = 2x - 3\\3x - 10x + 15 = 1\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = 2x - 3\\ - 7x =  - 14\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2.2 - 3\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;1} \right)\)

b) Nhân cả hai vế của phương trình thứ hai với \(\sqrt 2 \) ta được phương trình \(\sqrt 2 .\dfrac{1}{{\sqrt 2 }}x - \sqrt 2 .\sqrt 2 y = 3\sqrt 2 .\sqrt 2 \)\( \Leftrightarrow x - 2y = 6\) , khi đó

\(\left\{ \begin{array}{l}x - 2y = 6\\\dfrac{1}{{\sqrt 2 }}x - y\sqrt 2  = 3\sqrt 2 \end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x - 2y = 6\\x - 2y = 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}0 = 0\left( {lđ} \right)\\x - 2y = 6\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}y \in \mathbb{R}\\x = 2y + 6\end{array} \right.\)

Hệ phương trình có vô số nghiệm \(\left\{ \begin{array}{l}y \in \mathbb{R}\\x = 2y + 6\end{array} \right.\)

Câu 8

Phương pháp

Giải bài toán chuyển động bằng cách lập hệ phương trình

Ta sử dụng các công thức \(S = v.t\), \(v = \dfrac{S}{t},t = \dfrac{S}{v}\)

Với \(S:\) là quãng đường, \(v:\) là vận tốc, \(t\): thời gian

Lời giải 

Gọi thời gian vật đi trên mỗi đoạn đường AB và BC lần lượt là \(x\) phút và \(y\) phút (ĐK: \(y > x > 0\))

Vì vật đi từ A đến B với vận tốc 50 mét/phút rồi đi tiếp tứ B đến C với vận tốc 45 mét/phút thì tổng quãng đường đi được là 165m nên ta có phương trình \(50x + 45y = 165\)  (1)

Vì thời gian vật đi trên đoạn đường AB ít hơn thời gian vật đi trên đoạn đường BC là 30 giây\( = \dfrac{1}{2}\) phút nên ta có phương trình \(x + \dfrac{1}{2} = y\)  (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}50x + 45y = 165\\x + \dfrac{1}{2} = y\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}y = x + \dfrac{1}{2}\\50x + 45\left( {x + \dfrac{1}{2}} \right) = 165\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}y = x + \dfrac{1}{2}\\95x = \dfrac{{285}}{2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y = \dfrac{3}{2} + \dfrac{1}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y = 2\end{array} \right.\left( {TM} \right)\) 

Vậy thời gian vật đi trên mỗi đoạn đường AB và BC lần lượt là 1,5 phút và 2 phút.

 Loigiaihay.com