Đề kiểm tra 45 phút (1 tiết ) - Đề số 3 - Chương 2 - Hình học 8

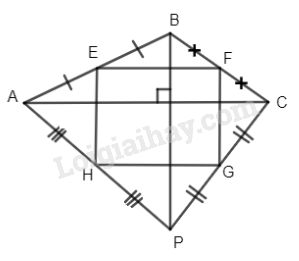
Đề bài

Bài 1. Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, AD. Tính diện tích tứ giác EFGH, biết AC = 8cm và BD = 6cm.

Bài 2. Cho hình bình hành ABCD, vẽ bốn điểm P, Q, R, S của các cạnh CD, AD, AB và BC. Chứng minh tứ giác tạo bởi các đường thẳng này có diện tích bằng \({1 \over 5}\) diện tích hình bình hành ABCD.

LG bài 1

Phương pháp giải:

Sử dụng tính chất đường trung bình của tam giác

Chứng minh tứ giác EFGH là hình chữ nhật

Lời giải chi tiết:

Ta có EF, HG lần lượt là các đường trung bình của \(\Delta ABC\) và \(\Delta ADC\) nên \({\rm{EF}}//HG//AC\) và EF = HG. Do đó tứ giác EFGH là hình bình hành.

Tương tự \(EH// BD\)mà \(BD \bot AC\left( {gt} \right) \Rightarrow {\rm{EF}} \bot {\rm{EH,}}\) do đó EFGH là hình chữ nhật và \(EF = {1 \over 2}AC = 4(cm),\) \(EH = {1 \over 2}BD = 3cm.\)

Vậy \({S_{EFGH}} = EF.EH = 12\left( {c{m^2}} \right).\)

LG bài 2

Phương pháp giải:

Nối A với C và chỉ ra các tam giác có cùng diên tích

Lời giải chi tiết:

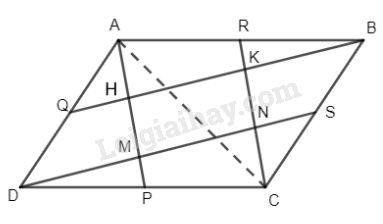
Nối A với C ta có AP là đường trung tuyến của \(\Delta ACD\) nên

\({S_{ADP}} = {S_{APC}} = {1 \over 2}{S_{ADC}} = {1 \over 4}{S_{ABCD}}\)

Tương tự \({S_{ACR}} = {S_{BCR}} = {1 \over 2}{S_{ABC}} = {1 \over 4}{S_{ABCD}}.\)

\( \Rightarrow {S_{APC}} + {S_{ACR}} = {S_{{\rm{AR}}CP}} = {1 \over 2}{S_{ABCD}}.\)

\({S_{ADP}} = {S_{APC}} = {1 \over 2}{S_{ADC}} = {1 \over 4}{S_{ABCD}}\)

Tương tự \({S_{ACR}} = {S_{BCR}} = {1 \over 2}{S_{ABC}} = {1 \over 4}{S_{ABCD}}.\)

\( \Rightarrow {S_{APC}} + {S_{ACR}} = {S_{{\rm{AR}}CP}} = {1 \over 2}{S_{ABCD}}.\)

Gọi H là giao điểm của AP và BQ, K là giao điểm của CR và BQ, M là giao điểm của AP và DS, N là giao điểm của CR và DS. 

Dễ thấy HKNM là hình bình hành nên các tam giác sau đây có cùng diện tích:

\({S_{AKH}} = {S_{HKM}} = {S_{MNH}} = {S_{MNC}} \)\(\,= {S_{AKB}} = {S_{MCD}}\)

Mà \({S_{AKR}} = {1 \over 2}{S_{AKB}}\) (đáy gấp đôi, chung đường cao)

Tương tự \({S_{MPC}} = {1 \over 2}{S_{MCD}}\)

\( \Rightarrow {S_{AKH}} = {S_{HKM}} = {S_{MNH}} \)\(\,= {S_{MNC}} = \left( {{S_{AKR}} + {S_{MPC}}} \right) \)\(\,= {1 \over 5}{S_{ARCP}}.\)

Mà \({S_{ARCP}} = {1 \over 2}{S_{ABCD}}\)

\( \Rightarrow {S_{HKM}} + {S_{MKN}} = {1 \over 5}{S_{ABCD}}\) hay \({S_{KHMN}} = {1 \over 5}{S_{ABCD}}.\)

Loigiaihay.com