Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 2 - Hình học 7

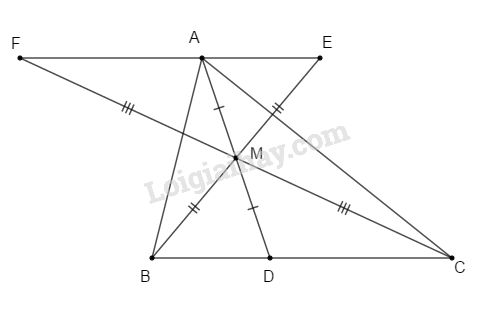
Đề bài

Bài 1. Cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Trên tia đối của tia MC lấy F sao cho MF = MC. Chứng minh:

a) AE = BD; 

b) AF // BC. 

c) Ba điểm A, E, F thẳng hàng.

Bài 2. Cho tam giác ABC cân tại A, M là trung điểm của BC.

a) Chứng minh \(\widehat {AFE} = \widehat {ABC} \Rightarrow EF//BC\) \(\Delta ABM = \Delta ACM\).

b) Chứng minh \(AM \bot BC.\)

c) Trên cạnh BA lấy  điểm E. Trên cạnh CA lấy điểm F sao cho BE = CF. Chứng minh \(\Delta EBC\) và \(\Delta FCB\) bằng nhau.

d) Chứng minh EF // BC.

LG bài 1

Phương pháp giải:

Sử dụng:

Hai góc đối đỉnh thì bằng nhau

Nếu 1 đường thẳng cắt hai đường thẳng tạo thành 1 cặp góc so le trong bằng nhau thì 2 đường thẳng đó song song với nhau

Tiên đề Ơ-Clít

Lời giải chi tiết:

a) Xét \(\Delta AEM\) và \(\Delta DBM\) có:

MA = MD (giả thiết)

\(\widehat {AME} = \widehat {DMB}\)(đối đỉnh)

ME = MB (giả thiết)

Do đó \(\Delta AEM\)= \(\Delta DBM\)(c.g.c)

\( \Rightarrow AE = DB.\)

b) Chứng minh tương tự câu a ta có:

\(\Delta AFM = \Delta DCM\)(c.g.c)

\( \Rightarrow \widehat {FAM} = \widehat {CDM}\)(góc tương ứng)

\( \Rightarrow AF//BC\) (1) (cặp góc so le trong bằng nhau).

c) Ta có \(\Delta AEM = \Delta DBM\)(chứng minh trên)

\( \Rightarrow \widehat {AEM} = \widehat {DBM} \Rightarrow AE//BC\)  (2).

Từ (1) và (2) \( \Rightarrow AE\) và AF trùng nhau (tiên đề Oclit) hay A, E, F thẳng hàng.

LG bài 2

Phương pháp giải:

Sử dụng:

Tổng của 2 góc kề bù bằng 180 độ

Tổng ba góc của 1 tam giác bằng 180 độ

Tam giác cân có hai góc ở đáy bằng nhau

Lời giải chi tiết:

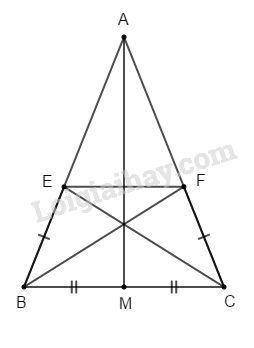
a) M là trung điểm của BC (giả thiết) \( \Rightarrow MB = MC.\)

Dễ thấy \(\Delta AMB = \Delta AMC\) (c.c.c)

b) \(\Delta AMB = \Delta AMC\)(chứng minh trên) \( \Rightarrow \widehat {AMB} = \widehat {AMC}\) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (kề bù) \( \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^o}\) hay \(AM \bot BC.\)

c) Xét \(\Delta EBC\) và \(\Delta FCB\) có:

+) BC chung

+) \(\widehat {EBC} = \widehat {FCB}\) (giả thiết)

+) \(BE = CF\) (giả thiết).

Do đó \(\Delta EBC = \Delta FCB\)(c.g.c)

d) Ta có:

\(AB = AC\) (giả thiết)

\(BE = CF\) (giả thiết)

\( \Rightarrow AB - BE = AC - CF\) hay \(AE = AF.\)

Do đó \(\Delta AEF\) cân tại A \( \Rightarrow \widehat {AEF} = \widehat {AFE} = \dfrac{{{{180}^o} - \widehat A} }{ 2}.\)

Tương tự ta có \(\Delta ABC\) cân tại A (giả thiết)

\( \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^o} - \widehat A}}{2}.\)

Vậy \(\widehat {AFE} = \widehat {ABC} \Rightarrow EF//BC\) (cặp góc đồng vị bằng nhau).

Loigiaihay.com