Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 3 - Hình học 7

Đề bài

Bài 1: Cho tam giác ABC biết BC = 1cm; AB = 6cm. Tính độ dài cạnh AC biết độ dài này là một số nguyên.

Bài 2: Chứng minh rằng “trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy”.

Bài 3: Cho tam giác ABC có AB = 6cm; AC = 12cm; BC = 15cm.

a) Chứng minh rằng \(\Delta ABC\) vuông.

b) Vẽ trung tuyến AM. Từ M vẽ MH vuông góc với AC. Trên tia đối của tia MH lấy điểm K sao cho MK = MH. Chứng minh \(\Delta MHC = \Delta MKB.\)

c) Gọi G là giao điểm của BH và AM. Gọi I là trung điểm của AB. Chứng minh rằng I, G, C thẳng hàng. 

LG bài 1

Phương pháp giải:

Trong một tam giác độ dài 1 cạnh luôn lớn hơn hiệu độ dài hai cạnh và nhỏ hơn tổng độ dài hai cạnh còn lại

Lời giải chi tiết:

Bài 1: Ta có \(6 - 1AC < 6 + 1\) hay \(5 < AC < 7\) mà độ dài AC là một số nguyên nên AC = 6cm.

LG bài 2

Phương pháp giải:

Trên tia đối của tia MA lấy D sao cho MD = MA

Chứng minh tam giác ABD bằng tam giác BAC

Lời giải chi tiết:

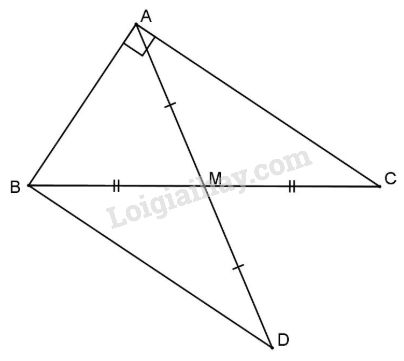
Trên tia đối của tia MA lấy D sao cho MD = MA khi đó ta có \(\Delta AMC = \Delta DMB\) (c.g.c)

\( \Rightarrow AC = B{\rm{D}}\) và \(\widehat C = {\widehat B_1}\)

\( \Rightarrow B{\rm{D}}\) // AC (có cặp góc so le trong bằng nhau)

Mà \(AC \bot AB\) (gt)

\( \Rightarrow B{\rm{D}} \bot AB\) hay \(\widehat {AB{\rm{D}}} = {90^0}\).

Xét hai tam giác vuông ABD và BAC có AB chung, AC = BD (cmt).

Do đó \(\Delta AB{\rm{D}} = \Delta BAC\) (c.g.c)

\( \Rightarrow A{\rm{D}} = BC\) mà \(AM = \dfrac{1}{ 2}A{\rm{D}} \Rightarrow AM = \dfrac{1 }{2}BC.\) 

LG bài 3

Phương pháp giải:

+Định lý Py-ta-go

+Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

+Ba đường trung tuyến của tam giác đồng quy tại trọng tam

Lời giải chi tiết:

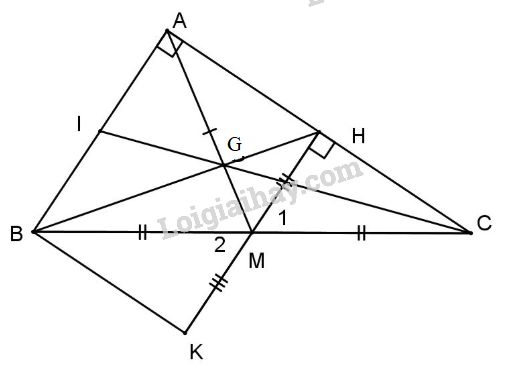
a) Ta có 

\(B{C^2} = A{B^2} + A{C^2}{\rm{    }}({15^2} = {9^2} + {12^2}).\)

Theo định lý Pytago đảo \(\Delta ABC\) vuông tại A.

b) Xét \(\Delta MHC\) và \(\Delta MKB\) có

+) MC = MB (gt);

+) \({\widehat M_1} = {\widehat M_2}\) (đối đỉnh);

+) MH = MK (gt).

Do dó \(\Delta MHC = \Delta MKB\) (c.g.c)

c) Vì tam giác ABC vuông tại A có AM là đường trung tuyến nên \(AM = MC = \dfrac{{BC}}{2}\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền) 

Suy ra tam giác AMC cân tại M có MH là đường cao nên MH cũng là đường trung tuyến

Hay H là trung điểm của AC

Xét tam giác ABC có 2 đường trung tuyến AM và BH giao nhau tại G nên G là trọng tâm tam giác. Lại có CI cũng là đường trung tuyến của tam giác ABC nên \(G\in CI\) hay I, G, C thẳng hàng. 

Loigiaihay.com