Đề kiểm tra 15 phút - Đề số 8 - Bài 9, 10 - Chương 1 - Hình học 8

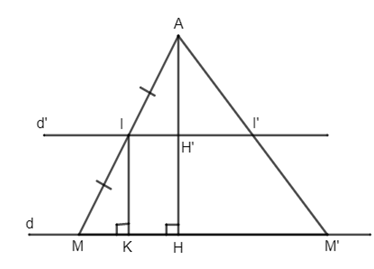
Đề bài

Cho điểm A nằm ngoài đường thẳng d. Tìm tập hợp các trung điểm của đoạn thẳng AM khi M di chuyển trên đường thẳng d.

Lời giải chi tiết

 

Gọi I là trung điểm của đoạn thẳng AM.

Kẻ IK, AH vuông góc với d \(\left( {K,H \in d} \right)\) .

Ta có \(IK//AH\) nên IK là đường trung bình của tam giác AHM

\( \Rightarrow IK = \dfrac{1 }{2}AH.\)

A, d cho trước nên khoảng cách từ A đến d là AH không đổi \( \Rightarrow IK\) không đổi mà \(K \in d \Rightarrow I\) thuộc đường thẳng \(d'\) song song với d và cách d một khoảng bằng \(\dfrac{{AH} }{ 2}.\)

Bây giờ lấy điểm \(I'\) thuộc \(d'\), \(AI'\)cắt d tại \(M'\). Vì \(I'H'//M'H\) và \(H'\) là trung điểm của AH nên \(H'I'\) là đường trung bình của \(\Delta AH'M \Rightarrow I'A = I'M'\) .

Vậy tập hợp các trung điểm I của đoạn AM khi M di động trên đường thẳng d là đường thẳng \(D'//d\) và cách d một đoạn bằng \(\dfrac{{AH} }{ 2}\) (AH là khoảng cách từ A đến d).

Loigiaihay.com