Đề kiểm tra 15 phút - Đề số 7 - Bài 7, 8 - Chương 2 - Hình học 7

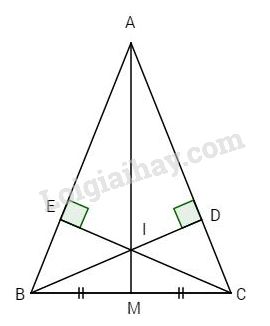
Đề bài

Cho tam giác ABC cân tại A, vẽ BD, CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm cả BD và CE.

a) Chứng minh rằng \(\Delta AEI = \Delta ADI.\)

b) Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.

Lời giải chi tiết

a) Xét tam giác  AEC và ADB có:

+) \(\widehat {AEC} = \widehat {ADB} = {90^o}\) (giả thiết)

+) AB = AC (giả thiết);

+) \(\widehat A\) chung

Vậy \(\Delta AEC = \Delta ADB\) (g.c.g)

\( \Rightarrow AE = AD\) (cạnh tương ứng).

Xét \(\Delta AEI\) và \(\Delta ADI\) có:

+) \(\widehat {AEI} = \widehat {ADI} = {90^O}\) (giả thiết)

+) \(AE = AD\) (chứng minh trên)

+) AI cạnh chung

Do đó \(\Delta AEI = \Delta ADI\) (ch.cgv).

b) M là trung điểm của BC (giả thiết) \( \Rightarrow MB = MC\)

Xét \(\Delta AMB \) và \( \Delta AMC\) có:

+) AM cạnh chung

+) \(AB = AC\) (giả thiết)

+) \(MB = MC\) (giả thiết)

Do đó \(\Delta AMB = \Delta AMC\) (c.c.c) \( \Rightarrow \widehat {BAM} = \widehat {CAM}\) (góc tương ứng) hay AM là phân giác của \(\widehat {BAC}\)

lại có \(\Delta AEI = \Delta ADI\) (chứng minh trên)

\( \Rightarrow \widehat {EAI} = \widehat {DAI}\) hay AI là phân giác của \(\widehat {BAC}\)

Hai điểm M và I cùng thuộc tia phân giác của góc BAC nên A, I, M thẳng hàng.

Loigiaihay.com