Đề kiểm tra 15 phút - Đề số 5 - Chương I - Giải Tích 12Đáp án và lời giải chi tiết Đề thi kiểm tra 15 phút - Đề số 5 - Chương I - Giải Tích 12 Quảng cáo
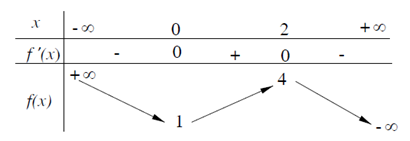
Đề bài Câu 1. Hàm số \(y = - {x^4} + 8{x^2} + 5\) nghịch biến trên khoảng nào ? A. \(( - \infty ;0)\) B. \(( - \infty ; - 2)\) và \((0;2)\) C. \((0; + \infty )\) D. \(( - 2;0)\) và \((2; + \infty )\). Câu 2. Cho hàm số \(y = f'(x)\) có bảng biến thiên như sau:
Khi đó, điểm cực đại của hàm số là A. x = 0. B. x = 4. C. x = 2. D. x = 1. Câu 3. Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{3}{{x - 2}}\) là A. 0 B. 1 C. 2 D. 3 Câu 4. Hệ số góc tiếp tuyến của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) tại điểm giao điểm của đồ thị với trục tung bằng: A. – 2 B. 2 C. 1 D. – 1. Câu 5. Tìm giá trị của m đề hàm số \(y = {x^3} - 3{x^2} + mx\) đạt cực tiểu tại x = 2. A. m = 0 B. m = 1 C. m = 3 D. m < 0. Câu 6. Phương trình tiếp tuyến của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) tại điểm có hoành độ bằng 3: A. \(y = 3x + 13\) B \(y = 3x - 5\) C. \(y = - 3x - 5\) D. \(y = - 3x + 13\). Câu 7. Cho hàm số \(y = x + \dfrac{4}{{x - 2}}\) , giá trị nhỏ nhất của hàm số trên [- 1 ; 1] là: A. – 4 B. – 3 C. – 7/3 D. – 2 . Câu 8. Cho hàm số \(y = {x^3} - 4{x^2} + 5x - 2\). Mệnh đề nào sau đây đúng ? A. Hàm số nghịch biến trên khoảng \(( - \infty ;1)\). B. Hàm số đồng biến trên khoảng \(\left( {1;\dfrac{5 }{ 3}} \right)\). C. Hàm số nghịch biến trên khoảng \(\left( {\dfrac{5 }{ 3}; + \infty } \right)\). D. Hàm số nghịch biến trên khoảng \(\left( {1;\dfrac{5 }{3}} \right)\). Câu 9. Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{5}{ {x - 1}}\) là đường thẳng có phương trình ? A. y = 5 B. x = 0 C. x = 1 D. y = 0 Câu 10. Cho hàm số \(y = {\dfrac{2018} {x - 2}}\) có đồ thị (C). Số đường tiệm cận của (C) là: A. 0 B. 2 C. 3 D. 1 Lời giải chi tiết
Câu 1. Ta có \(y' = - 4{x^3} + 16x,\,\,y' = 0\) \(\Rightarrow - 4{x^3} + 16x = 0\,\, \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\\x = 2\end{array} \right.\) Ta có bảng biến thiên:
Từ bbt ta thấy hàm số nghịch biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\). Chọn D. Câu 2. Điểm cực đại của hàm số là x=2. Chọn C. Câu 3. Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0,\) \(\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty ,\,\mathop {\lim }\limits_{x \to {2^ - }} y= - \infty \,\). Do đó đường tiệm cận đứng của đồ thị hàm số là x = 2, đường tiệm cận nagng của đồ thị hàm số là y = 0. Vậy đồ thị hàm số có hai đường tiệm cận. Chọn đáp án C. Câu 4. Giao điểm của đồ thị hàm số với trục tung có x = 0. Ta có \(y' = \dfrac{{x + 1 - \left( {x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{2}{{{{\left( {x + 1} \right)}^2}}},\) \(y'(0) = 2\). Do đó hệ số góc tiếp tuyến của đồ thị hàm số bằng 2. Chọn đáp án B. Câu 5. Để hàm số đạt cực tiểu tại x = 2 thì \(\left\{ \begin{array}{l}y'(2) = 0\,\,\\y''(2) > 0\end{array} \right.\). Ta có \(y' = 3{x^2} - 6x + m\) \(\Rightarrow \,{3.2^2} - 6.2 + m = 0\, \Rightarrow m = 0\) và do \(y'' = 6x - 6,\,\,y''(2) = 6 > 0\) nên với m = 0 thì hàm số đạt cực tiểu tại x = 2. Câu 6. Ta có \(y' = \dfrac{{x - 2 - \left( {x + 1} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \dfrac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} \) \(\Rightarrow \,\,y'(3) = - 3\,,\,\,y(3) = 4\). Từ đó, phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 3 là : \(y = - 3\left( {x - 3} \right) + 4 = - 3x + 13\). Chọn đáp án D. Câu 7. Ta có \(D = R\backslash \{ 2\} ,\,\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty ,\) \(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \). Đồ thị hàm số có đường tiệm cận đứng là x = 2. \(y' = \dfrac{{{x^2} - 4x}}{{{{\left( {x - 2} \right)}^2}}},\,\,y' = 0\) \(\Rightarrow \,\,{x^2} - 4x = 0 \Leftrightarrow \,\,\left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\) Ta có bảng biến thiên :
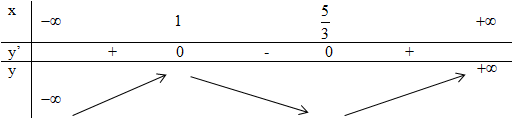
Vậy giá trị nhỏ nhất của hàm số trên [- 1;1] là – 3 . Chọn đán án B. Câu 8. Ta có \(y' = 3{x^2} - 8x + 5,\,y' = 0\, \) \(\Rightarrow \,\,3{x^2} - 8x + 5 = 0\, \Leftrightarrow \,\,\left[ \begin{array}{l}x = 1\\x = \dfrac{5}{3}\end{array} \right.\) . Ta có bảng biến thiên:
Chọc đáp án D. Câu 9. Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0\) nên đường tiệm cận ngang của đồ thị hàm số đã cho là y = 0. Chọn đáp án D. Câu 10. Ta có \(\begin{array}{l}D = R\backslash \{ 2\} \\\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0,\\ \mathop {\lim }\limits_{x \to {2^ + }} y = + \infty ,\,\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \end{array}\) Do đó đồ thị hàm số có đường tiệm cận đứng là \(x = 2\), đường tiệm cận ngang là \(y = 0\). Vậy có đồ thị hàm số đã cho có hai đường tiệm cận. Chọn đáp án B. Loigiaihay.com
|






















Danh sách bình luận