Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 7

Đề bài

Bài 1:  Cho góc vuông \(\widehat {xOy},\)điểm M nằm trong góc đó. Vẽ điểm N và P sao cho Ox là đường trung trực của MN và Oy là đường trung trực của MP. Chứng minh ON = OP. 

Bài 2: Cho góc \(\widehat {xOy}\) tù, bên ngoài góc đó dựng tia Oz vuông góc với Ox và Ot vuông góc với Oy. Chứng tỏ rằng : \( \widehat {xOy} + \widehat {tOz} = {180^o}.\)

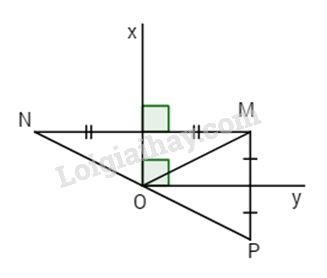
Lời giải chi tiết

Bài 1:  

Ox là đường trung trực của đoạn MN nên \(OM = ON.\)

Oy là đường trung trực của đoạn MP nên \(OM = OP\)

Vậy \(ON = OP.\)

Bài 2:

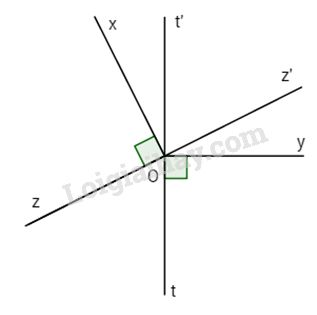
Vẽ Oz’ và Ot’ lần lượt là tia đối của các tia Oz và Ot, ta có: \(\widehat {t'Oz'}= \widehat {tOz}\) (đối đỉnh)

\(\widehat {xOz} = \widehat {t'Oy} = {90^o}.\)

\(\begin{array}{l}
\Rightarrow \widehat {xOz} + \widehat {t'Ox} = \widehat {t'Oy} + \widehat {t'Ox}\\
\Rightarrow \widehat {zOt'} = \widehat {xOy}
\end{array}\)

Mà \(\widehat {zOt'} + \widehat {t'Oz'} = {180^o}\) (vì Oz’ là tia đối của tia Oz)

\( \Rightarrow \widehat {xOy} + \widehat {tOz} = {180^o}.\)

Loigiaihay.com