Đề kiểm tra 15 phút - Đề số 4 - Bài 11 - Chương 1 - Hình học 8

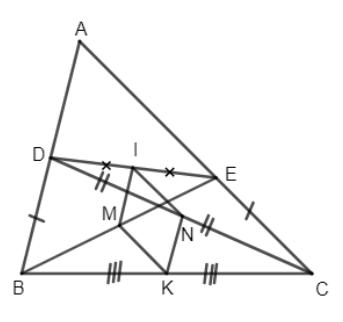
Đề bài

Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE, BC. Chứng minh rằng: \(IK \bot MN.\)

Lời giải chi tiết

Ta có M là trung điểm của BE

I là trung điểm của DE

\( \Rightarrow MI\) là đường trung bình của \(\Delta BDE\)

\( \Rightarrow MI//BD\) và \(MI = \dfrac{1}{2}BD\)

Lại có NK là đường trung bình của tam giác CBD (do N là trung điểm CD và K là trung điểm BC) nên \(NK//BD\) và \(NK = \dfrac{1}{2}BD\)

Do đó \(MI//NK\) nên tứ giác MINK là hình bình hành (1)

Ta có IN là đường trung bình của \(\Delta CDE\) (do I là trung điểm DE và N là trung điểm DC)

\( \Rightarrow IN = \dfrac{1 }{ 2}CE\) mà CE = BD (gt) \( \Rightarrow IN = IM\)   (2)

Từ (1) và (2) \( \Rightarrow \) Tứ giác MINK là hình thoi (hình bình hành có hai cạnh kề bằng nhau)

Loigiaihay.com