Đề kiểm tra 15 phút - Đề số 3 - Chương I - Hình học 12

Đề bài

Câu 1: Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Khi đó tỷ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:

\(A.\,\,\dfrac{1}{4}\)          \(B.\,\,\dfrac{1}{8}\) 

\(C.\,\,\dfrac{1}{2}\)          \(D.\,\,\dfrac{1}{6}\)

Câu 2: Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a thể tích của (H) bằng:

\(A.\,\,\dfrac{{{a^3}\sqrt 2 }}{3}\)     \(B.\,\,\dfrac{{{a^3}}}{2}\)

\(C.\,\,\dfrac{{{a^3}\sqrt 3 }}{4}\)     \(D.\,\,\dfrac{{{a^3}\sqrt 2 }}{2}\)

Câu 3: Cho hình trụ có bán kính bằng 5, khoảng cách giữa hai đáy bằng 7. Diện tích toàn phần của hình trụ bằng:

\(A.\,\,10\pi \)           

\(C.\,\,85\pi \)     

\(D.\,\,95\pi \)

Câu 4: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho \(SA' = \dfrac{1}{3}SA\). Mặt phẳng qua A' và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lầ lượt tại B', C', D'. Khi đó thể tích hình chóp S.A'B'C'D' bằng:

\(A.\,\,\dfrac{V}{{27}}\)        \(B.\,\,\dfrac{V}{{81}}\)

\(C.\,\,\dfrac{V}{9}\)        \(D.\,\,\dfrac{V}{3}\)

Câu 5: Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và \(\widehat {A\,\,} = {60^0}\) . Chân đường cao hạ từ B' xuống (ABCD) trùng với giao điểm 2 đường chéo, biết BB' = a. Thể tích khối lăng trụ là:

\(A.\,\,\dfrac{{3{a^3}}}{2}\)              \(B.\;\dfrac{{3{a^3}}}{8}\)

\(C.\;\dfrac{{3{a^3}}}{4}\)                \(D.\;\dfrac{{{a^3}}}{4}\)

Câu 6: Thể tích khối tứ diện đều có cạnh bằng 1 là:

\(A.\,\,\dfrac{{\sqrt 2 }}{4}\)         \(B.\,\,\dfrac{{\sqrt 2 }}{6}\)

\(C.\,\,\dfrac{{\sqrt 2 }}{{12}}\)        \(D.\,\,\dfrac{{\sqrt 3 }}{4}\)

Câu 7: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, AA′ = c.
Gọi M và N theo thứ tự là trung điểm của A'B' và B'C'. Tỉ số giữa thể tích của khối chóp D'.DMN và thể tích khối hộp chữ nhật ABCD.A'B'C'D' là: 

\(A.\,\,\dfrac{1}{2}\)          \(B.\,\,\dfrac{1}{6}\)

\(C.\,\,\dfrac{1}{8}\)          \(D.\,\,\dfrac{1}{4}\)

Câu 8: Cho hình chóp S.ABCD. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. khi đó tỉ số về thể tích: \(\dfrac{{{V_{S.A'B'C;}}}}{{{V_{S.ABC}}}}\) được tính bằng:

\(A.\,\,\dfrac{1}{2}.\dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)

\(B.\,\,\dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)

\(C.\,\,\dfrac{{SA}}{{SA'}}.\dfrac{{SB}}{{SB'}}.\dfrac{{SC}}{{SC'}}\)

\(D.\,\,\dfrac{1}{3}.\dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)

Lời giải chi tiết

Câu 1:

Ta có: \(\dfrac{{{V_{A.B'C'D}}}}{{{V_{A.BCD}}}} = \dfrac{{AB'}}{{AB}}.\dfrac{{AC'}}{{AC}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\)

Chọn đáp án A.

Câu 2:

Ta có: \({S_d} = \dfrac{1}{2}a.a.\sin {60^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \(V = a.{S_d} = \dfrac{{{a^3}\sqrt 3 }}{4}\)

Chọn đáp án C.

Câu 3:

Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi .5\left( {5 + 7} \right)\)\(\, = 120\pi \)

Chọn đáp án B.

Câu 4:

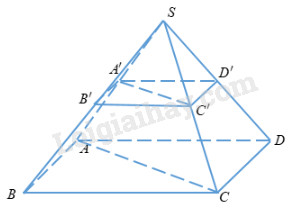
Ta có: \(SA' = \dfrac{1}{3}SA \)

\(\Rightarrow \left\{ \begin{array}{l}SB' = \dfrac{1}{3}SB\\SC' = \dfrac{1}{3}SC\\SD' = \dfrac{1}{3}SD\end{array} \right.\)

Khi đó ta có:

\(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}} \)

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}} \)

\(\Rightarrow {V_{S.A'B'C'}} = \dfrac{1}{{27}}{V_{S.ABC}}\)

\(\dfrac{{{V_{S.A'D'C'}}}}{{{V_{S.ADC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SD'}}{{SD}}.\dfrac{{SC'}}{{SC}}\)

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}} \)

\(\Rightarrow {V_{S.A'D'C'}} = \dfrac{1}{{27}}{V_{S.ADC}}\)

\( \Rightarrow {V_{S.A'B'C'D'}} = {V_{S.A'B'C'}} + {V_{S.A'D'C'}} \)\(\,= \dfrac{1}{{27}}\left( {{V_{S.ABC}} + {V_{S.ADC}}} \right) = \dfrac{V}{{27}}\)

Chọn đáp án A.

Câu 5:

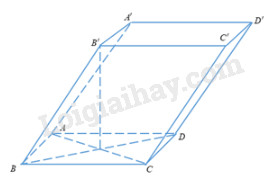
Gọi O là giao điểm của AC và BD

Xét tam giác ABD có \(\left\{ \begin{array}{l}AB = AD\\\widehat A = {60^ \circ }\end{array} \right.\)

\( \Rightarrow \Delta ABD\) là tam giác đều

Hay \(AB = AD = BD = a \Rightarrow BO = \dfrac{a}{2}\)

Khi đó \(B'O = \sqrt {B{{B'}^2} - B{O^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  \)\(\,= \dfrac{{a\sqrt 3 }}{2}\)

\( \Rightarrow V = B'O.{S_{ABCD}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}.2.a \)\(\,= \dfrac{{3{a^3}}}{2}\)

Chọn đáp án A.

Câu 6:

Diện tích đáy: \(S = \dfrac{{\sqrt 3 }}{4}\)

Đường cao: \(h = \sqrt {1 - \dfrac{1}{3}}  = \dfrac{{\sqrt 6 }}{3}\)

Khi đó \(V = \dfrac{1}{3}.\dfrac{{\sqrt 3 }}{4}.\dfrac{{\sqrt 6 }}{3} = \dfrac{{\sqrt 2 }}{{12}}\)

Chọn đáp án C.

Câu 7:

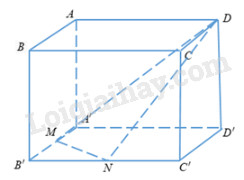
Ta có: \({V_{ABCD.A'B'C'D'}} = abc\)

+ \({S_{D'MN}} = {S_{A'B'C'D'}} - {S_{A'D'M}} - {S_{D'C'N}} - {S_{B'MN}} \)

\(= ab - \dfrac{1}{2}\dfrac{a}{2}b - \dfrac{1}{2}a.\dfrac{b}{2} - \dfrac{1}{2}\dfrac{a}{2}\dfrac{b}{2}\)\(\, = \dfrac{3}{8}ab\)

Khi đó: \({V_{D.D'MN}} = \dfrac{1}{3}.c.\dfrac{3}{8}ab = \dfrac{1}{8}abc \)

\(\Rightarrow \dfrac{{{V_{D.D'MN}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{{\dfrac{1}{8}abc}}{{abc}} = \dfrac{1}{8}\)

Chọn đáp án C.

Câu 8:

Ta có: \(\dfrac{{{V_{S.A'B'C}}}}{{{V_{S.ABC}}}} = \,\dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)

Chọn đáp án B.

Loigiaihay.com