Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 7 Quảng cáo
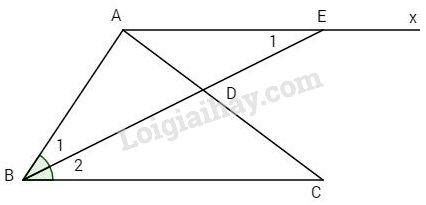
Đề bài Cho tam giác ABC có \(\widehat B = {60^o}\), phân giác BD. Từ A kẻ Ax song song với BC cắt tia BD tại E. a) Chứng minh rằng \(\Delta ABE\) cân. b) Tính \(\widehat {BAE}\). Phương pháp giải - Xem chi tiết Nếu 1 đường thẳng cắt hai đường thẳng song song thì: Các cặp góc so le trong bằng nhau. Đường phân giác của 1 góc chia đôi góc đó thành 2 góc bằng nhau Tam giác cân có hia góc ở đáy bằng nhau Tổng ba góc của 1 tam giác bằng 180 độ Lời giải chi tiết
a) Ta có Ax // BC \( \Rightarrow \widehat {{B_2}} = \widehat {{E_1}}\) (cặp góc so le trong), mà \(\widehat {{B_2}} = \widehat {{B_1}}\)(giả thiết) \( \Rightarrow \widehat {{B_1}} = \widehat {{E_1}}\). Chứng tỏ \(\Delta ABE\) cân tại A. b) BD là phân giác của góc \(\widehat B = {60^o}\) \(\Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{ 2}\widehat B = {30^o}\). \(\Delta ABE\) cân tại A \( \Rightarrow \widehat {{E_1}} = \widehat {{B_1}} = {30^o}\). Mà \(\widehat {BAE} + \widehat {{E_1}} + \widehat {{B_1}} = {180^o}\) \(\Rightarrow \widehat {ABE} = {180^o} - \left( {\widehat {{E_1}} + \widehat {{B_1}}} \right) \)\(\,= {180^o} - \left( {{{30}^o} + {{30}^o}} \right) = {120^o}.\) Loigiaihay.com
|




















Danh sách bình luận