Đề kiểm tra 15 phút - Chương 1 - Đề số 2 - Đại số 10Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 2 - Đại số 10 Quảng cáo
Đề bài Chọn phương án đúng Câu 1. Tìm câu không phải mệnh đề A. Số 2009 chia hết cho 3. B. Phở rất ngon! C. Hà Nội là thủ đô của nước Thái Lan. D. 2+3=10. Câu 2. Tìm mệnh đề sai A. \(\Delta ABC\) đều \( \Leftrightarrow AB=AC\) và \(\widehat A\)= \(60^\circ \). B. \(n \;\vdots \;3 \Leftrightarrow {n^2} \;\vdots\; 3\). C. \(ABCD\) là hình chữ nhật \( \Leftrightarrow AC = BD\). D. \(n \;\vdots \;6 \Leftrightarrow n\; \vdots \;2\) và \(n\; \vdots\; 3\). Câu 3. Cho mệnh đề chứa biến \(P(x)\) “\({x^2}-5x + 6 = 0\)”, với \(x \in \mathbb{R}\). Tìm mệnh đề đúng A. P(1) B. P(6) C. P(2) D. P(-1) Câu 4. Tìm mệnh đề đúng A. \(\forall n \in \mathbb{N},{{\rm{n}}^2}+1\) không chia hết cho 3. B. \(\forall x \in \mathbb{R},{\rm{ (x - 1}}{{\rm{)}}^2} \ne x - 1\). C. \(\exists n \in \mathbb{N},{\rm{ }}{{\rm{n}}^2} + 1\) chia hết cho 4. D. \(\exists x \in \mathbb{Q},{\rm{ }}{{\rm{x}}^2} = 2009\). Câu 5. Tìm mệnh đề sai A. \(\forall n \in \mathbb{N},{\rm{ 2n}} \ge {\rm{n}}{\rm{.}}\) B. \(\forall x \in \mathbb{R},{\rm{ }}{{\rm{x}}^2} + 1 \ne x.\) C. \(\exists n \in \mathbb{N},{\rm{ }}{{\rm{n}}^2} = n\) D. \(\forall x \in \mathbb{R},{\rm{ }}{{\rm{x}}^2} > 0\) Câu 6. Tìm mệnh đề phủ định của mệnh đề “\(\exists x \in \mathbb{R},{\rm{ 3x = }}{{\rm{x}}^2} + 1\)” A. \(\exists x \in \mathbb{R},{\rm{ 3x = }}{{\rm{x}}^2} + 1\) B. \(\forall x \in \mathbb{R},{\rm{ 3x = }}{{\rm{x}}^2} + 1\) C. \(\exists x \in \mathbb{R},{\rm{ 3x > }}{{\rm{x}}^2} + 1\) D. \(\forall x \in \mathbb{R},{\rm{ 3x}} \ne {x^2} + 1\) Câu 7. Liệt kê các phần tử của tập \(S{\rm{ = }}\left\{ {x \in \mathbb{R}|(x - 1)(2{x^2} - 5x + 3) = 0} \right\}\). A. \(S=\left\{ {1;1;\dfrac{3}{2}} \right\}\) B. \(S=\left\{ {1;\dfrac{3}{2}} \right\}\) C. \(S=\left\{ {\dfrac{3}{2}} \right\}\) D. \(S=\left\{ 1 \right\}\) Câu 8. Tập nào sau đây là tập rỗng ? A. \(A=\left\{ {x \in \mathbb{R}|(x - 1)({x^2} + 4x + 5) = 0} \right\}\) B. \(B=\left\{ {x \in \mathbb{R}|5x = {x^2} + 6} \right\}\) C. \(C = \left\{ {x \in \mathbb{Q}|{x^2} - (\sqrt 2 + 1)x + \sqrt 2 = 0} \right\}\) D. \(D = \left\{ {n \in \mathbb{N}|3{n^2} + 5n + 2 = 0} \right\}\) Câu 9. Cho \(M = \left\{ {x \in \mathbb{R}|f(x) = 0} \right\},\)\(\,N = \left\{ {x \in \mathbb{R}|g(x) = 0} \right\},\) \(P = \left\{ {x \in \mathbb{R}|f(x)g(x) = 0} \right\}.\) Khi đó A.\(P = M \cup N\) B. \(P = M \cap N\) C. \(P = M\backslash N\) D. \(P = N\backslash M\) Câu 10. Cho A, B là các tập tùy ý. Tìm mệnh đề đúng A. \(A \cap B = A\) B. \(A \cup B = B\) C. \((A\backslash B) \cup (B\backslash A) = (A \cup B)\backslash (A \cap B)\) D. \((A\backslash B) \cup B = A\) Lời giải chi tiết
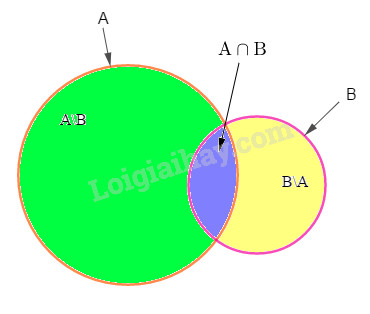
Câu 1. Chọn B. Đây là câu cảm thán nên không phải là mệnh đề. Câu 2. Chọn C. Không phải là mệnh đề tương đương, chỉ là mệnh đề kéo theo. Câu 3. Chọn C. Thay \(x = 2\) ta được: \(2^2-5.2+6=0\) nên \(P\left( 2 \right)\) là mệnh đề đúng. Câu 4. Chọn A. Xét các trường hợp + Nếu \(n=3k\) thì \({n^2} + 1 = 9{k^2} + 1\) không chia hết cho 3. + Nếu \(n = 3k \pm 1\) thì \(\begin{array}{l}{n^2} + 1 = {\left( {3k \pm 1} \right)^2} + 1\\{\rm{ }} = 9{k^2} \pm 6k + 1 + 1\\{\rm{ }} = 3k\left( {3k + 2} \right) + 2\end{array}\) không chia hết cho 3. Vậy \(\forall n \in \mathbb{N},{n^2} + 1\) không chia hết cho 3. Câu 5. Chọn D. Tồn tại x=0 sao cho x2=0. Câu 6. Chọn D. Áp dụng: Phủ định của mệnh đề “\(\exists x \in X,P(x)\)” là mệnh đề “\(\forall x \in X,\overline {P(x)} \) “. Ta có: Phủ định của mệnh đề \(\exists x \in R,3x = {x^2} + 1\) là \(\forall x \in \mathbb{R},{\rm{ 3x}} \ne {x^2} + 1\). Câu 7. Chọn B. Ta có: \(\begin{array}{l}\left( {x - 1} \right)\left( {2{x^2} - 5x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\2{x^2} - 5x + 3 = 0\end{array} \right.\\{\rm{ }} \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1{\rm{ \text{ hoặc } x = }}\dfrac{3}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{3}{2}\end{array} \right.\end{array}\) Vậy \(S = \left\{ {1;\dfrac{3}{2}} \right\}\) . Câu 8. Chọn D. \(3{n^2} + 5n + 2 = 0\) \(\Leftrightarrow n = - 1{\rm{ \text{ hoặc } n = }}\dfrac{{ - 2}}{3}\) Cả hai giá trị này đều bị loại vì không phải số tự nhiên. Vậy \(D = \emptyset \) . Câu 9. Chọn A Ta có \(\begin{array}{l}x \in P \Leftrightarrow f(x)g(x) = 0\\{\rm{ }} \Leftrightarrow f(x) = 0{\rm{ }}\text{ hoặc }{\rm{ }}g(x) = 0\\{\rm{ }} \Leftrightarrow x \in M{\rm{\text{ hoặc } x}} \in {\rm{N}} \Leftrightarrow x \in M \cup N\end{array}\) Vậy \(P = M \cup N\) . Câu 10. Chọn C Kiểm tra hệ thức \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left( {A \cup B} \right)\backslash \left( {A \cap B} \right)\) bằng biểu đồ Ven. Bằng cách tương tự kiểm tra được các hệ thức còn lại sai. Loigiaihay.com
|




















Danh sách bình luận