Đề kiểm tra 15 phút - Đề số 16 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 16 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7 Quảng cáo
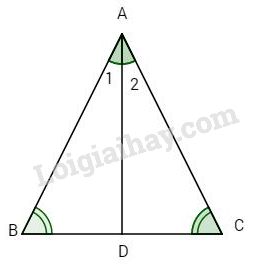
Đề bài Cho tam giác ABC có \(\widehat B = \widehat C\). Tia phân giác của góc A cắc BC tại D. Chứng minh: a) \(\Delta ADB = \Delta ADC\) b) \(AD \bot BC\) Phương pháp giải - Xem chi tiết Tổng ba góc trong một tam giác bằng 180 độ Tổng hai góc kề bù bằng 180 độ Lời giải chi tiết
a) Xét ta \(\Delta ADB \) có \(\widehat {{A_1}} + \widehat B + \widehat {ADB} = {180^o}\) \( \Rightarrow \widehat {ADB} = {180^o} - \left( {\widehat {{A_1}} + \widehat B} \right).\) Tương tự với \( \Delta ADC\) ta có \(\widehat {ADC} = {180^o} - \left( {\widehat {{A_2}} + \widehat C} \right)\) Mà \(\widehat {{A_1}} = \widehat {{A_2}},\,\widehat B = \widehat C\) (giả thiết) \( \Rightarrow \widehat {ADB} = \widehat {ADC}\) Xét \(\Delta ADB \) và \( \Delta ADC\) có +) \(\widehat {{A_1}} = \widehat {{A_2}}\)(giả thiết) +) AD cạnh chung; +) \(\widehat {ADB} = \widehat {ADC}\) (chứng minh trên) \(\Rightarrow \Delta ADB = \Delta ADC\) (g.c.g). b) Ta có \(\widehat {ADB} = \widehat {ADC}\) (chứng minh trên), mà \(\widehat {ADB} + \widehat {ADC} = {180^o}\)(cặp góc kề bù) \( \Rightarrow \widehat {ADB} = \widehat {ADC} = {90^o}\). Chứng tỏ \(AD \bot BC\). Loigiahay.com
|




















Danh sách bình luận