Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3Đề bài
Câu 1 :
Trong các hình sau:  Các hình có thể là hình biểu diễn của một hình tứ diện là:
Câu 2 :
Chọn khẳng định sai trong các khẳng định sau?
Câu 3 :
Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD.\) Giao tuyến của hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right)\) là:
Câu 4 :
Chọn mệnh đề đúng
Câu 5 :
Tìm mệnh đề đúng trong các mệnh đề sau:
Câu 6 :
Cho hình bình hành $ABCD.$ Gọi $Bx, Cy, Dz$ là các đường thẳng song song với nhau lần lượt đi qua $B, C, D$ và nằm về một phía của mặt phẳng $(ABCD),$ đồng thời không nằm trong mặt phẳng $(ABCD).$ Một mặt phẳng đi qua $A$ và cắt $Bx, Cy, Dz$ lần lượt tại các điểm $B’, C’, D’ $ với $BB’ = 2, DD’ = 4.$ Khi đó $CC’$ bằng:
Câu 7 :
Cho tứ diện $ABCD.$ Gọi $M,N,P,Q$ lần lượt là trung điểm $AC, BC, BD, AD.$ Tìm điều kiện của tứ diện $ABCD$ để $MNPQ$ là hình thoi?
Câu 8 :
Cho tứ diện \(ABCD\,.\) Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(AB\) và \(AC,\) \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC.\) Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\) và tứ diện \(ABCD\) là:
Câu 9 :
Cho đường thẳng $d$ và mặt phẳng $\left( \alpha \right)$ . Một mặt phẳng $\left( \beta \right)$ chứa $d$ và cắt $\left( \alpha \right)$ theo giao tuyến là đường thẳng $d'$ . Giao điểm của $d$ và $d'$ là $A$ . Khẳng định nào sau đây là sai?
Câu 10 :
Cho \(d//\left( \alpha \right)\) và \(d' \subset \left( \alpha \right)\), số giao điểm của \(d\) và \(d'\) là:
Câu 11 :
Mệnh đề nào dưới đây đúng?
Câu 12 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Lời giải và đáp án
Câu 1 :
Trong các hình sau:  Các hình có thể là hình biểu diễn của một hình tứ diện là:
Đáp án : D Lời giải chi tiết :
Hình (III) có thể là hình tứ diện. Vì nếu ta nhìn từ điểm C hướng xuống BD thì B, C, D thẳng hàng. Hình (IV) có thể là hình tứ diện. Vì nếu điểm C nằm phía trước mặt phẳng (ABD) thì ta có thể nhìn thấy các đường CA, CB, CD, do đó các đường này là nét liền. Chú ý
Một số em có thể chỉ chọn đáp án A vì nghĩ các hình \(\left( {II} \right), (III), \left( {IV} \right)\) không biểu diễn tứ diện là sai.
Câu 2 :
Chọn khẳng định sai trong các khẳng định sau?
Đáp án : B Lời giải chi tiết :
Hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó, chúng có vô số đường thẳng chung \( \Rightarrow \) B sai.
Câu 3 :
Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD.\) Giao tuyến của hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right)\) là:
Đáp án : C Phương pháp giải :
- Tìm một điểm chung dễ thấy của hai mặt phẳng. - Tìm điểm chung thứ hai bằng cách tìm hai đường thẳng lần lượt thuộc hai mặt phẳng mà chúng cắt nhau. Lời giải chi tiết :
 \( \bullet \) \(B\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right).\) \( \bullet \) Vì \(M,N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD\) nên suy ra \(AN,{\rm{ }}DM\) là hai trung tuyến của tam giác \(ACD.\) Gọi \(G = AN \cap DM\) \( \Rightarrow \left\{ \begin{array}{l}G \in AN \subset \left( {ABN} \right) \Rightarrow G \in \left( {ABN} \right)\\G \in DM \subset \left( {MBD} \right) \Rightarrow G \in \left( {MBD} \right)\end{array} \right. \Rightarrow G\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right).\) Vậy \(\left( {ABN} \right) \cap \left( {MBD} \right) = BG.\)
Câu 4 :
Chọn mệnh đề đúng
Đáp án : A Lời giải chi tiết :
Tính chất của hai đường thẳng song song: - Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó. - Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. Từ hai tính chất trên ta thấy chỉ có đáp án A đúng. Chú ý
Một số em có thể sẽ chọn nhầm đáp án C vì quên mất hai đường thẳng đó phải phân biệt. Một số em khác có thể sẽ chọn nhầm đáp án D vì không xét đến trường hợp điểm đó nằm trên đường thẳng thì sẽ không tồn tại đường thẳng nào đi qua điểm đó mà song song với đường thẳng đã cho.
Câu 5 :
Tìm mệnh đề đúng trong các mệnh đề sau:
Đáp án : D Lời giải chi tiết :
Hai đường thẳng phân biệt nếu không có điểm chung (không cắt nhau) thì có thể song song hoặc chéo nhau nên A, B, C sai, D đúng.
Câu 6 :
Cho hình bình hành $ABCD.$ Gọi $Bx, Cy, Dz$ là các đường thẳng song song với nhau lần lượt đi qua $B, C, D$ và nằm về một phía của mặt phẳng $(ABCD),$ đồng thời không nằm trong mặt phẳng $(ABCD).$ Một mặt phẳng đi qua $A$ và cắt $Bx, Cy, Dz$ lần lượt tại các điểm $B’, C’, D’ $ với $BB’ = 2, DD’ = 4.$ Khi đó $CC’$ bằng:
Đáp án : D Phương pháp giải :
- Đưa về cùng mặt phẳng; - Sử dụng các tính chất của đường trung bình của tam giác, đường trung bình của hình thang. Lời giải chi tiết :
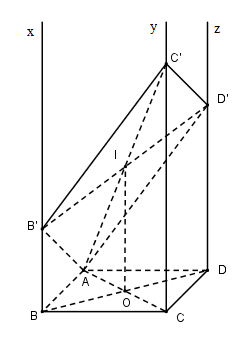 Trên $Bx$ và $Dz$ lấy điểm $B’$ và $D’$ sao cho $BB’ = 2, DD’ = 4.$ Gọi $O$ là tâm hình bình hành $ABCD, I $ là trung điểm của $B’D’$ Ta có $BDD’B’$ là hình thang, $OI$ là đường trung bình của hình thang nên $OI // BB’ // DD’ // Cy$ và \(OI = \dfrac{{BB' + {\rm{DD}}'}}{2} = \dfrac{{2 + 4}}{2} = 3\). Xét mặt phẳng tạo bởi $OI$ và $CC’$ có: \(AI \cap Cy = C'\). Ta có $OI // CC’, AO = OC$ suy ra $AI = IC’$ Suy ra $OI$ là đường trung bình của tam giác $ACC’$ \( \Rightarrow CC' = 2OI = 6\)
Câu 7 :
Cho tứ diện $ABCD.$ Gọi $M,N,P,Q$ lần lượt là trung điểm $AC, BC, BD, AD.$ Tìm điều kiện của tứ diện $ABCD$ để $MNPQ$ là hình thoi?
Đáp án : D Phương pháp giải :
- Đưa về cùng mặt phẳng. - Sử dụng các tính chất đường trung bình của tam giác - Các dấu hiệu nhận biết hình bình hành, hình thoi. Lời giải chi tiết :
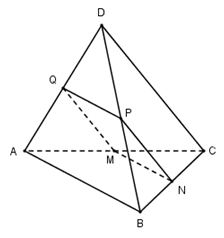 Vì $MN$ và $PQ$ lần lượt là đường trung bình của tam giác $ABC$ và $ABD$ nên: \(\left\{ \begin{array}{l}MN//PQ//AB\\MN = PQ = \dfrac{1}{2}AB\end{array} \right. \Rightarrow \) MNPQ là hình bình hành. Để $MNPQ $ trở thành hình thoi ta cần thêm yếu tố $MN = PN.$ Ta có: $PN$ là đường trung bình của tam giác $BCD$ nên \(PN = \dfrac{1}{2}CD\). $MN = PN $ \( \Leftrightarrow \dfrac{1}{2}AB = \dfrac{1}{2}CD \Leftrightarrow AB = CD.\) Vậy để $MNPQ $ là hình thoi cần thêm điều kiện $AB = CD.$
Câu 8 :
Cho tứ diện \(ABCD\,.\) Gọi \(M,\,\,N\) lần lượt là trung điểm các cạnh \(AB\) và \(AC,\) \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC.\) Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\) và tứ diện \(ABCD\) là:
Đáp án : D Phương pháp giải :
Sử dụng định lý ba giao tuyến song song: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến, nếu có hai đường thẳng song song thì đường thẳng thứ ba cũng song song với chúng. Lời giải chi tiết :
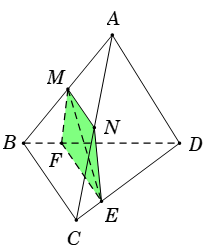 Tam giác \(ABC\) có \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC\,.\) Suy ra \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow \,\,MN\)//\(BC\,.\) Từ \(E\) kẻ đường thẳng \(d\) song song với \(BC\) và cắt \(BD\) tại \(F\,\, \Rightarrow \,\,EF\)//\(BC.\) Do đó \(MN//EF\) suy ra bốn điểm \(M,\,\,N,\,\,E,\,\,F\) đồng phẳng và \(MNEF\) là hình thang. Vậy hình thang \(MNEF\) là thiết diện cần tìm.
Câu 9 :
Cho đường thẳng $d$ và mặt phẳng $\left( \alpha \right)$ . Một mặt phẳng $\left( \beta \right)$ chứa $d$ và cắt $\left( \alpha \right)$ theo giao tuyến là đường thẳng $d'$ . Giao điểm của $d$ và $d'$ là $A$ . Khẳng định nào sau đây là sai?
Đáp án : D Phương pháp giải :
Ta tìm giao tuyến của đường thẳng $b$ và mặt phẳng $\left( \alpha \right)$ : + Tìm một mặt phẳng chứa $b$ thích hợp + Tìm giao tuyến của mặt phẳng này với mặt phẳng $\left( \alpha \right)$ + Tìm giao điểm của giao tuyến đó với đường thẳng $b$ Lời giải chi tiết :
Vì $A \in d'$ mà $d' \subset \left( \alpha \right)$ và $d' \subset \left( \beta \right)$ nên $A \in \left( \alpha \right)$ và \(A \in \left( \beta \right)\) Vì $A$ là giao điểm của $d$ và $d'$ nên $A \in d$ Mà $A \in \left( \alpha \right)$ nên $A$ là giao điểm của $d$ và $\left( \alpha \right)$
Câu 10 :
Cho \(d//\left( \alpha \right)\) và \(d' \subset \left( \alpha \right)\), số giao điểm của \(d\) và \(d'\) là:
Đáp án : C Lời giải chi tiết :
Vì \(d//\left( \alpha \right)\) và \(d' \subset \left( \alpha \right)\) nên \(d\) và \(d'\) chỉ có thể song song hoặc chéo nhau. Do đó chũng không có điểm chung.
Câu 11 :
Mệnh đề nào dưới đây đúng?
Đáp án : C Phương pháp giải :
Sử dụng các kiến thức về đường thẳng song song với đường thẳng và đường thẳng song song với mặt phẳng. Lời giải chi tiết :
A và D sai vì hai đường thẳng cùng song song với một mặt phẳng thì hai đường thẳng đó song song với nhau hoặc trùng nhau. B sai vì hai đường thẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
Câu 12 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Đáp án : C Phương pháp giải :
- Tính chất đường thẳng song song với mặt phẳng. - Định lí đường trung bình của tam giác. Lời giải chi tiết :
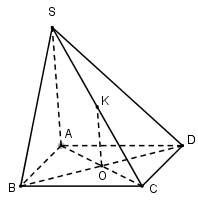 Gọi $O$ là giao điểm của $AC$ và $BD$ Trong mặt phẳng $SAC,$ qua $O$ kẻ ${\rm{O}}K \bot AC\,\,\left( {K \in SC} \right)$, suy ra $mp$\(\left( \alpha \right)\) chính là $mp(BDK).$ $OK // SA ; AO = OC$\( \Rightarrow \) $SK = KC.$ (Định lí đường trung bình của tam giác) |



















Danh sách bình luận