Đề kiểm tra 1 tiết Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2

Đề bài

Câu 1 :

Cho hình chóp $S.ABCD $ có đáy $ABCD$ là hình vuông với $AC = \dfrac{{a\sqrt 2 }}{2}$. Cạnh bên $SA$ vuông góc với đáy, $SB$ hợp với đáy góc ${60^0}$. Tính khoảng cách $d$ giữa hai đường thẳng $AD$ và $SC.$

A

$d = \dfrac{{a\sqrt 3 }}{4}.$
B

$d = \dfrac{{a\sqrt 2 }}{2}.$
C

$d = \dfrac{a}{2}.$
D

$d = \dfrac{{a\sqrt 3 }}{2}.$

Câu 2 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$. Mệnh đề nào sau đây đúng?

A

$\varphi = {30^0}.$
B

$\sin \varphi = \dfrac{{\sqrt 5 }}{5}.$
C

$\varphi = {60^0}.$
D

$\sin \varphi = \dfrac{{2\sqrt 5 }}{5}.$

Câu 3 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ và $SA = SB = SC = b$. Gọi $G$ là trọng tâm $\Delta ABC$. Độ dài $SG$ là:

A

$\dfrac{{\sqrt {9{b^2} + 3{a^2}} }}{3}$.
B

$\dfrac{{\sqrt {{b^2} - 3{a^2}} }}{3}$.
C

$\dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}$.
D

$\dfrac{{\sqrt {{b^2} + 3{a^2}} }}{3}$.

Câu 4 :

Cho hình chóp S.ABCD có đáy là hình thang vuông $\left( {AB//CD} \right)$; SD vuông góc với mặt đáy $\left( {ABCD} \right);{\rm{ }}AD = 2a;{\rm{ }}SD = a\sqrt 2 .$ Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).

A

$\dfrac{{2a}}{{\sqrt 3 }}$
B

$\dfrac{a}{{\sqrt 2 }}$
C

$a\sqrt 2 $
D

$\dfrac{{a\sqrt 3 }}{2}$

Câu 5 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,$ tam giác $SAD $ đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách $d$ giữa hai đường thẳng $SA$ và $BD.$

A

$d = \dfrac{{a\sqrt {21} }}{{14}}.$
B

$d = \dfrac{{a\sqrt 2 }}{2}.$
C

$d = \dfrac{{a\sqrt {21} }}{7}.$
D

$d = a$

Câu 6 :

Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:

A

Ba mặt phẳng $\left( ABC \right),\,\,\left( ABD \right),\,\,\left( ACD \right)$ đôi một vuông góc.
B

Hình chiếu của A lên mặt phẳng $\left( BCD \right)$ là trực tâm của tam giác BCD.
C

Tam giác BCD vuông.
D

Hai cạnh đối của tứ diện vuông góc.

Câu 7 :

Cho hình chóp $S.ABC$ có $SA \bot (ABC)$ và $AB \bot BC.$ Số các mặt của tứ diện $S.ABC$ là tam giác vuông là:

A

$1.$
B

$3.$
C

$2.$
D

$4.$

Câu 8 :

Cho hình chóp $A.BCD$ có cạnh $AC \bot \left( {BCD} \right)$ và $BCD$ là tam giác đều cạnh bằng $a.$ Biết $AC = a\sqrt 2 $ và $M$ là trung điểm của $BD.$ Khoảng cách từ $C$ đến đường thẳng $AM$ bằng

A

$a\sqrt {\dfrac{7}{5}} .$
B

$a\sqrt {\dfrac{4}{7}} .$
C

$a\sqrt {\dfrac{6}{{11}}} .$
D

$a\sqrt {\dfrac{2}{3}} .$

Câu 9 :

Cho $\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 5$, góc giữa $\overrightarrow a $ và $\overrightarrow b $ bằng $120^\circ $. Chọn khẳng định sai trong các khẳng định sau?

A

$\left| {\vec a + \vec b} \right| = \sqrt {19} $
B

$\left| {\vec a - \vec b} \right| = 7$
C

$\left| {\vec a - 2\vec b} \right| = \sqrt {139} $
D

$\left| {\vec a + 2\vec b} \right| = 9$

Câu 10 :

Mệnh đề nào sau đây là đúng?

A

Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B

Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau
C

Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau
D

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia

Câu 11 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a,\,\,\,SA \bot \left( {ABC} \right),\,\,\,SA = \dfrac{{a\sqrt 3 }}{2}.$ Gọi $\left( P \right)$ là mặt phẳng đi qua $A$ và vuông góc với $BC.$ Thiết diện của hình chóp $S.ABC$ được cắt bởi $\left( P \right)$ có diện tích bằng ?

A

$\dfrac{{3{a^2}}}{8}.$
B

$\dfrac{{3{a^2}}}{2}.$
C

$\dfrac{{3{a^2}}}{4}.$
D

$\dfrac{{2{a^2}}}{3}.$

Câu 12 :

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ song song với nhau và một điểm $M$ không thuộc $\left( P \right)$ và $\left( Q \right)$. Qua $M$ có bao nhiêu mặt phẳng vuông góc với $\left( P \right)$ và $\left( Q \right)$?

A

$2.$
B

$3.$
C

$1.$
D

Vô số

Câu 13 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác cạnh $BC = a,\,\,AC = 2a\sqrt 2 $, góc $\widehat {ACB} = {45^0}$. Cạnh bên $SB$ vuông góc với mặt phẳng $(ABC).$ Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBC).$

A

$\dfrac{{2a}}{3}.$
B

$2a.$
C

$\dfrac{{8a}}{3}.$
D

$\dfrac{{3a}}{4}.$

Câu 14 :

Trong mặt phẳng $\left( \alpha \right)$ cho tứ giác $ABCD$ và một điểm $S$ tùy ý. Mệnh đề nào sau đây đúng?

A

$\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {CD} $.
B

$\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {CD} $(Với $S$ là điểm tùy ý).
C

Nếu $\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} $ thì $ABCD$ là hình bình hành
D

$\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $ khi và chỉ khi $O$ là giao điểm của $AC$ và $BD$.

Câu 15 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = a,{\rm{ }}AC = a\sqrt 3 $. Tam giác $SBC$ đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $\left( {SAC} \right)$.

A

$d = \dfrac{{a\sqrt {39} }}{{13}}.$
B

$d = a.$
C

$d = \dfrac{{2a\sqrt {39} }}{{13}}.$
D

$d = \dfrac{{a\sqrt 3 }}{2}.$

Câu 16 :

Cho tứ diện $ABCD$ có $AB \bot CD$ và $AC \bot BD$. Gọi $H$ là hình chiếu vuông góc của $A$ lên $mp(BCD)$. Các khẳng định sau, khẳng định nào sai?

A

$H$ là trực tâm tam giác $BCD$.
B

$CD \bot (ABH)$.
C

$AD \bot BC$.
D

Các khẳng định trên đều sai.

Câu 17 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Tam giác $SAB$ đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy $\left( {ABCD} \right)$. Biết hình chiếu của $S$ lên mặt phẳng đáy trùng với trung điểm của $AB$. Gọi $\varphi $ là góc giữa $SD$ và mặt phẳng $\left( {ABCD} \right)$. Mệnh đề nào sau đây đúng?

A

$\cot \varphi = \dfrac{5}{{\sqrt {15} }}.$
B

$\cot \varphi = \dfrac{{\sqrt {15} }}{5}.$
C

$\varphi = {30^0}.$
D

$\cot \varphi = \dfrac{{\sqrt 3 }}{2}.$

Câu 18 :

Cho hình chóp đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tâm $O$; $SO = 2a$. Gọi $M$ là điểm thuộc đoạn $AO{\rm{ }}\,\left( {M \ne A;M \ne O} \right)$. Mặt phẳng $\left( \alpha \right)$ đi qua $M$ và vuông góc với $AO$. Đặt $AM = x$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp $S.ABC.$

A

$S = 2{a^2}.$
B

$S = 2{x^2}.$
C

$S = \dfrac{{\sqrt 3 }}{2}{\left( {a - x} \right)^2}.$
D

$S = 2{\left( {a - x} \right)^2}.$

Câu 19 :

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có các cạnh $AB = 2,\,\,AD = 3;\,AA' = 4$. Góc giữa hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ là $\alpha $. Tính giá trị gần đúng của góc $\alpha $?

A

$45,2^\circ $.
B

$38,1^\circ $.
C

$53,4^\circ $.
D

$61,6^\circ $.

Câu 20 :

Cho hình chóp $S.ABC$ trong đó $SA$, $AB$, $BC$ vuông góc với nhau từng đôi một. Biết $SA = 3a$, $AB = a\sqrt 3 $, $BC = a\sqrt 6 $. Khoảng cách từ $B$ đến $SC$ bằng

A

$a\sqrt 2 $.
B

$2a$.
C

$2a\sqrt 3 $.
D

$a\sqrt 3 $.

Câu 21 :

Cho hình lập phương ABCD. A’B’C’D’ có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB’D’) và (BC’D) bằng:

A

$\dfrac{{\sqrt 3 }}{3}$
B

$\dfrac{2}{{\sqrt 3 }}$
C

$\dfrac{{\sqrt 3 }}{2}$
D

$\sqrt 3 $

Câu 22 :

Cho hình chóp $S.ABC $ có đáy $ABC$ là tam giác vuông tại $B, AB = 3a, BC = 4a.$ Cạnh bên $SA$ vuông góc với đáy. Góc tạo bởi giữa $SC$ và đáy bằng ${60^0}$. Gọi $M$ là trung điểm của $AC,$ tính khoảng cách $d$ giữa hai đường thẳng $AB$ và $SM.$

A

$d = a\sqrt 3 .$
B

$d = 5a\sqrt 3 .$
C

$d = \dfrac{{5a}}{2}.$
D

$d = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.$

Câu 23 :

Cho hình chóp $S.ABCD$, có đáy $ABCD$ là hình chữ nhật. Cạnh bên $SA$ vuông góc với đáy, $SA = AB = a$ và $AD = x.a$. Gọi $E$ là trung điểm của $SC$. Tìm $x$, biết khoảng cách từ điểm $E$ đến mặt phẳng $\left( {SBD} \right)$ bằng $h = \dfrac{a}{3}$.

A

$1.$
B

$\sqrt 2 .$
C

$2.$
D

$4.$

Câu 24 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Cạnh bên $SA$ vuông góc với mặt phẳng đáy và có độ dài bằng $a\sqrt 2 $. Gọi $\alpha $ là góc giữa hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBD} \right)$. Tính $\cos \alpha $.

A

$\cos \alpha = \dfrac{3}{5}$.
B

$\cos \alpha = \dfrac{{\sqrt 6 }}{3}$.
C

$\cos \alpha = \dfrac{{2\sqrt 2 }}{5}$.
D

$\cos \alpha = \dfrac{{\sqrt {10} }}{5}$.

Câu 25 :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a$, $AD = a\sqrt 3 $. Cạnh bên $SA = 2a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ đi qua $A$ vuông góc với $SC$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp đã cho.

A

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{7}.$
B

${S_{AMIN}} = \dfrac{{12{a^2}\sqrt 6 }}{{35}}.$
C

${S_{AMIN}} = \dfrac{{6{a^2}\sqrt 6 }}{{35}}.$
D

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{5}.$

Lời giải và đáp án

Câu 1 :

A

$d = \dfrac{{a\sqrt 3 }}{4}.$
B

$d = \dfrac{{a\sqrt 2 }}{2}.$
C

$d = \dfrac{a}{2}.$
D

$d = \dfrac{{a\sqrt 3 }}{2}.$

Đáp án : A

Phương pháp giải :

Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng

Lời giải chi tiết :

Ta có $SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}$

Tam giác $ABC$ vuông cân tại $B$ nên $AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{a}{2}$

Xét tam giác vuông $SAB $ có : $SA = AB.\tan {60^0} = \dfrac{a}{2}.\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}$

Ta có $d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)$

Kẻ $AK \bot SB$.

Do $\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK$, mà $AK \bot SB$ nên $AK \bot \left( {SBC} \right)$

Khi đó

$d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 3 }}{4}$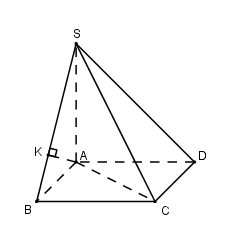

Câu 2 :

A

$\varphi = {30^0}.$
B

$\sin \varphi = \dfrac{{\sqrt 5 }}{5}.$
C

$\varphi = {60^0}.$
D

$\sin \varphi = \dfrac{{2\sqrt 5 }}{5}.$

Đáp án : D

Phương pháp giải :

Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

Lời giải chi tiết :

Gọi $M$ là trung điểm của $BC$, suy ra $AM \bot BC$

Ta có $\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM$

$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;AM} \right)} = \widehat {SMA}.$

Tam giác $ABC$ đều cạnh $a$, suy ra trung tuyến $AM = \dfrac{{a\sqrt 3 }}{2}.$

Tam giác vuông $SAM$, có $\sin \widehat {SMA} = \dfrac{{SA}}{{SM}} = \dfrac{{SA}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{2\sqrt 5 }}{5}.$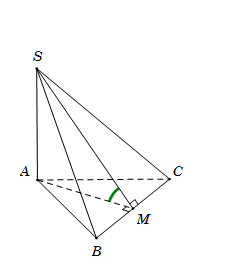

Câu 3 :

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ và $SA = SB = SC = b$. Gọi $G$ là trọng tâm $\Delta ABC$. Độ dài $SG$ là:

A

$\dfrac{{\sqrt {9{b^2} + 3{a^2}} }}{3}$.
B

$\dfrac{{\sqrt {{b^2} - 3{a^2}} }}{3}$.
C

$\dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}$.
D

$\dfrac{{\sqrt {{b^2} + 3{a^2}} }}{3}$.

Đáp án : C

Phương pháp giải :

- Sử dụng tính chất hình chóp đều: Hình chiếu của đỉnh lên mặt đáy là trọng tâm của tam giác đáy.

- Từ đó tính được độ dài $SG$ dựa vào mối quan hệ giữa cạnh và góc trong tam giác vuông.

Lời giải chi tiết :

Theo bài ra hình chóp $S.ABC$ là hình chóp tam giác đều.

Gọi $H$ là trung điểm của $BC$, ta có $SG \bot (ABC),G \in AH$.

Mà $AH = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AG = \dfrac{2}{3}AH = \dfrac{{a\sqrt 3 }}{3}$.

Tam giác $SAG$ vuông tại $G$ nên theo định lý Pi-ta-go ta có :

$SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{{3{b^2} - {a^2}}}{3}} = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}$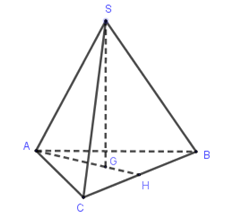

Câu 4 :

A

$\dfrac{{2a}}{{\sqrt 3 }}$
B

$\dfrac{a}{{\sqrt 2 }}$
C

$a\sqrt 2 $
D

$\dfrac{{a\sqrt 3 }}{2}$

Đáp án : A

Phương pháp giải :

Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.

$d\left( {CD;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$

Lời giải chi tiết :

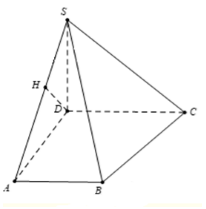Do $AB//CD$ do đó $d\left( {CD;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$

Dựng $DH \bot SA$ ta có:

$\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{AB \bot AD}\\{AB \bot SD}\end{array}} \right. \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow AB \bot DH}\\{\left\{ {\begin{array}{*{20}{l}}{DH \bot AB}\\{DH \bot SA}\end{array}} \right. \Rightarrow DH \bot \left( {SAB} \right) \Rightarrow d\left( {D;\left( {SAB} \right)} \right) = DH}\end{array}$

Áp dụng hệ thức lượng trong tam giác vuông

$ \Rightarrow d = DH = \dfrac{{SD.DA}}{{\sqrt {S{D^2} + D{A^2}} }} = \dfrac{{2a}}{{\sqrt 3 }}$

Câu 5 :

A

$d = \dfrac{{a\sqrt {21} }}{{14}}.$
B

$d = \dfrac{{a\sqrt 2 }}{2}.$
C

$d = \dfrac{{a\sqrt {21} }}{7}.$
D

$d = a$

Đáp án : C

Phương pháp giải :

Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng

Lời giải chi tiết :

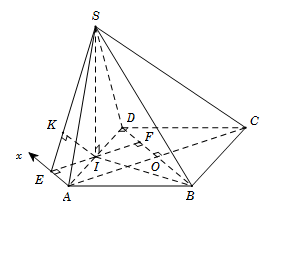Gọi $I$ là trung điểm của $AD$ nên suy ra $SI \bot AD \Rightarrow SI \bot \left( {ABCD} \right)$ và $SI = \dfrac{{a\sqrt 3 }}{2}$

Kẻ $Ax\parallel BD$. Do đó $d\left( {BD;SA} \right) = d\left( {BD;\left( {SAx} \right)} \right) = d\left( {D;\left( {SAx} \right)} \right) = 2d\left( {I;\left( {SAx} \right)} \right)$

(vì $DI \cap \left( {SAx} \right) = A$ và $IA = \dfrac{1}{2}DA$)

Kẻ $IE \bot Ax$, kẻ $IK \bot SE\,\,\left( 1 \right)$ ta có:

$\left\{ \begin{array}{l}Ax \bot SI\\Ax \bot IE\end{array} \right. \Rightarrow Ax \bot \left( {SIE} \right) \Rightarrow Ax \bot IK\,\,\left( 2 \right)$

Từ (1) và (2) $ \Rightarrow IK \bot \left( {SAx} \right)$. Khi đó $d\left( {I;\left( {SAx} \right)} \right) = IK$

Gọi $F$ là hình chiếu của $I$ trên $BD$, ta dễ dàng chứng minh được $\Delta IAE = \Delta IDF\left( {ch - gn} \right) $ $\Rightarrow IE = IF = \dfrac{{AO}}{2} = \dfrac{{a\sqrt 2 }}{4}$

Tam giác vuông $SIE$, có $IK = \dfrac{{SI.IE}}{{\sqrt {S{I^2} + I{E^2}} }} = \dfrac{{a\sqrt {21} }}{{14}}$

Vậy $d\left( {BD;SA} \right) = 2IK = \dfrac{{a\sqrt {21} }}{7}.$

Câu 6 :

Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc. Chỉ ra mệnh đề sai trong các mệnh đề sau:

A

Ba mặt phẳng $\left( ABC \right),\,\,\left( ABD \right),\,\,\left( ACD \right)$ đôi một vuông góc.
B

Hình chiếu của A lên mặt phẳng $\left( BCD \right)$ là trực tâm của tam giác BCD.
C

Tam giác BCD vuông.
D

Hai cạnh đối của tứ diện vuông góc.

Đáp án : C

Phương pháp giải :

Xét tính đúng sai của từng đáp án, sử dụng lý thuyết của hai mặt phẳng vuông góc: Một đường thẳng vuông góc với mặt phẳng này thì mọi mặt phẳng chứa đường thẳng đều vuông góc với mặt phẳng đã cho.

Lời giải chi tiết :

$\begin{array}{l}\left\{ \begin{array}{l}AD \bot AB\\AD \bot AC\end{array} \right. \Rightarrow AD \bot \left( {ABC} \right) \Rightarrow \left( {ACD} \right) \bot \left( {ABC} \right);\left( {ABD} \right) \bot \left( {ABC} \right)\\\left\{ \begin{array}{l}AC \bot AD\\AC \bot AB\end{array} \right. \Rightarrow AC \bot \left( {ABD} \right) \Rightarrow \left( {ACD} \right) \bot \left( {ABD} \right)\end{array}$

$\Rightarrow $ A đúng.

$AD\bot \left( ABC \right)\Rightarrow AD\bot BC$. Tương tự ta chứng minh được

$AB\bot CD;\,\,AC\bot BD\Rightarrow D$ đúng.

Gọi H là trực tâm của tam giác BCD ta có $\left\{ \begin{align} DH\bot BC \\ AD\bot BC \\ \end{align} \right.\Rightarrow BC\bot \left( ADH \right)\Rightarrow AH\bot BC$

Tương tự ta chứng minh được $AH\bot BD;\,\,AH\bot CD\Rightarrow AH\bot \left( BCD \right)$ $\Rightarrow $ B đúng.

Chưa đủ điều kiện để kết luận tam giác $BCD$ vuông.

Câu 7 :

Cho hình chóp $S.ABC$ có $SA \bot (ABC)$ và $AB \bot BC.$ Số các mặt của tứ diện $S.ABC$ là tam giác vuông là:

A

$1.$
B

$3.$
C

$2.$
D

$4.$

Đáp án : D

Phương pháp giải :

Chứng minh tam giác $SBC$ vuông bằng cách chứng minh $SB \bot BC$, sử dụng phương pháp chứng minh hai đường thẳng vuông góc.

Lời giải chi tiết :

Có $AB \bot BC \Rightarrow \Delta ABC$ là tam giác vuông tại $B.$

Ta có $SA \bot (ABC) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AC\end{array} \right. \Rightarrow \Delta SAB,\Delta SAC$ là các tam giác vuông tại $A.$

Mặt khác $\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC$ là tam giác vuông tại $B.$

Vậy bốn mặt của tứ diện đều là tam giác vuông.

Câu 8 :

A

$a\sqrt {\dfrac{7}{5}} .$
B

$a\sqrt {\dfrac{4}{7}} .$
C

$a\sqrt {\dfrac{6}{{11}}} .$
D

$a\sqrt {\dfrac{2}{3}} .$

Đáp án : C

Phương pháp giải :

- Dựng hình chiếu $H$ của $C$ trên $AM$.

- Sử dụng các hệ thức trong tam giác vuông để tính $CH$

Lời giải chi tiết :

Dựng hình chiếu $H$ của $C$ trên $AM$

Do $\Delta BCD$ đều cạnh $a$ nên đường cao $MC = \dfrac{{a\sqrt 3 }}{2}$

$d\left( {C,AM} \right) = CH = \dfrac{{AC.MC}}{{\sqrt {A{C^2} + M{C^2}} }} = \dfrac{{a\sqrt {66} }}{{11}}$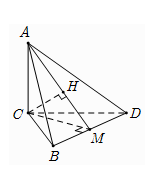

Câu 9 :

A

$\left| {\vec a + \vec b} \right| = \sqrt {19} $
B

$\left| {\vec a - \vec b} \right| = 7$
C

$\left| {\vec a - 2\vec b} \right| = \sqrt {139} $
D

$\left| {\vec a + 2\vec b} \right| = 9$

Đáp án : D

Phương pháp giải :

Sử dụng các hằng đẳng thức bình phương của tổng, hiệu và công thức tích vô hướng của hai véc tơ để tính độ dài các véc tơ ở mỗi đáp án.

Lời giải chi tiết :

Đáp án A: ${\left| {\vec a + \vec b} \right|^2} = {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\vec a^2} + {\vec b^2} + 2\vec a.\vec b $ $ = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$ $ = {3^2} + {5^2} + 2.3.5.\left( { - \dfrac{1}{2}} \right) = 19$

Do đó $\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {19} $

Đáp án B: ${\left| {\vec a - \vec b} \right|^2} = {\left( {\overrightarrow a - \overrightarrow b } \right)^2}$$ = {\overrightarrow a ^2} - 2\overrightarrow a \overrightarrow b + {\overrightarrow b ^2}$ $ = {\left| {\overrightarrow a } \right|^2} - 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) + {\left| {\overrightarrow b } \right|^2}$ $ = {3^2} - 2.3.5.\left( { - \dfrac{1}{2}} \right) + {5^2} = 49$ $ \Rightarrow \left| {\overrightarrow a - \overrightarrow b } \right| = 7$ nên B đúng.

Đáp án C: ${\left| {\overrightarrow a - 2\overrightarrow b } \right|^2} = {\left( {\overrightarrow a - 2\overrightarrow b } \right)^2}$ $ = {\overrightarrow a ^2} - 4\overrightarrow a \overrightarrow b + 4{\overrightarrow b ^2}$ $ = {\left| {\overrightarrow a } \right|^2} - 4\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) + 4{\left| {\overrightarrow b } \right|^2}$ $ = {3^2} - 4.3.5.\left( { - \dfrac{1}{2}} \right) + {4.5^2} = 139$ $ \Rightarrow \left| {\overrightarrow a - 2\overrightarrow b } \right| = \sqrt {139} $ nên C đúng.

Đáp án D: ${\left| {\overrightarrow a + 2\overrightarrow b } \right|^2} = {\left( {\overrightarrow a + 2\overrightarrow b } \right)^2}$ $ = {\overrightarrow a ^2} + 4\overrightarrow a \overrightarrow b + 4{\overrightarrow b ^2}$ $ = {\left| {\overrightarrow a } \right|^2} + 4\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) + 4{\left| {\overrightarrow b } \right|^2}$ $ = {3^2} + 4.3.5.\left( { - \dfrac{1}{2}} \right) + {4.5^2} = 79$ $ \Rightarrow \left| {\overrightarrow a + 2\overrightarrow b } \right| = \sqrt {79} $ nên D sai.

Câu 10 :

Mệnh đề nào sau đây là đúng?

A

Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B

Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau
C

Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau
D

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia

Đáp án : D

Lời giải chi tiết :

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

Câu 11 :

A

$\dfrac{{3{a^2}}}{8}.$
B

$\dfrac{{3{a^2}}}{2}.$
C

$\dfrac{{3{a^2}}}{4}.$
D

$\dfrac{{2{a^2}}}{3}.$

Đáp án : C

Phương pháp giải :

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, cụ thể là tính diện tích

Lời giải chi tiết :

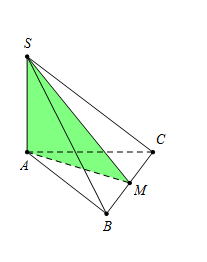Gọi $M$ là trung điểm của $BC$ thì $BC \bot AM\,\,\,\,\,\,\,\,\,\left( 1 \right).$

Hiển nhiên $AM = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 $.

Mà $SA \bot \left( {ABC} \right) \Rightarrow BC \bot SA\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$

Từ $\left( 1 \right)\,$và $\left( 2 \right)$ suy ra $BC \bot \left( {SAM} \right) \Rightarrow \left( P \right) \equiv \left( {SAM} \right).$

$ \Rightarrow $ Thiết diện của hình chóp $S.ABC$ được cắt bởi $(P)$ chính là $\Delta SAM.$

Và $\Delta \,SAM$ vuông tại $A$ nên ${S_{\Delta SAM}} = \dfrac{1}{2}SA.AM $ $= \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a\sqrt 3 = \dfrac{{3{a^2}}}{4}.$

Câu 12 :

A

$2.$
B

$3.$
C

$1.$
D

Vô số

Đáp án : D

Lời giải chi tiết :

Gọi $d$ là đường thẳng qua $M$ và vuông góc với $\left( P \right)$. Do $\left( P \right)\,\,\parallel \,\,\left( Q \right) \Rightarrow d \bot \left( Q \right)$.

Giả sử $\left( R \right)$ là mặt phẳng chứa $d$. Mà $\left\{ \begin{array}{l}d \bot \left( P \right)\\d \bot \left( Q \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( R \right) \bot \left( P \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right.$.

Có vô số mặt phẳng $\left( R \right)$ chứa $d$. Do đó có vô số mặt phẳng qua $M$, vuông góc với $\left( P \right)$ và $\left( Q \right)$.

Câu 13 :

A

$\dfrac{{2a}}{3}.$
B

$2a.$
C

$\dfrac{{8a}}{3}.$
D

$\dfrac{{3a}}{4}.$

Đáp án : B

Phương pháp giải :

Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng

Lời giải chi tiết :

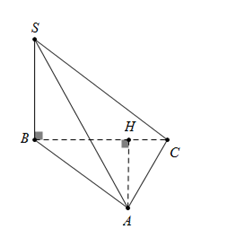Từ A kẻ AH vuông góc với $BC,\,\,H \in BC$ (1)

Ta có $SB$ vuông góc với $\left( {ABC} \right)$$ \Rightarrow SB \bot AH\,\,\,\left( 2 \right)$

Từ (1), (2) suy ra $AH \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH.$

Tam giác $AHC$ vuông tại $H$, có $\sin \widehat {HCA} = \dfrac{{AH}}{{AC}}$.

$ \Rightarrow AH = \sin \widehat {HAC}.AC = \sin {45^0}.AC = 2a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = 2a.$

Câu 14 :

Trong mặt phẳng $\left( \alpha \right)$ cho tứ giác $ABCD$ và một điểm $S$ tùy ý. Mệnh đề nào sau đây đúng?

A

$\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {CD} $.
B

$\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {CD} $(Với $S$ là điểm tùy ý).
C

Nếu $\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} $ thì $ABCD$ là hình bình hành
D

$\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $ khi và chỉ khi $O$ là giao điểm của $AC$ và $BD$.

Đáp án : C

Lời giải chi tiết :

A. Sai vì $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AB} + \overrightarrow {CD} \Leftrightarrow \overrightarrow {AC} - \overrightarrow {AB} + \overrightarrow {DC} - \overrightarrow {DB} = \overrightarrow 0 \Leftrightarrow B \equiv C$ (Vô lí)

B. Sai vì: Gọi $O$ và $O'$ theo thứ tự là trung điểm của $AC$ và $BD$. Ta có

$\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} $ và $\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO'} \Leftrightarrow \overrightarrow {SO} = \overrightarrow {SO'} \Leftrightarrow O \equiv O'$ điều này không đúng nếu $ABCD$ không phải là hình bình hành.

C. Đúng – Chứng minh tương tự như ý B.

D. sai vì: Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Khi đó:

$\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \\
\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {ON} \\
\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \\
\Leftrightarrow 2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 \\
\Leftrightarrow \overrightarrow {OM} + \overrightarrow {ON} = \overrightarrow 0
\end{array}$

Hay $O$ là trung điểm $MN$. Điều này chưa chắc đúng nên D sai.

Câu 15 :

A

$d = \dfrac{{a\sqrt {39} }}{{13}}.$
B

$d = a.$
C

$d = \dfrac{{2a\sqrt {39} }}{{13}}.$
D

$d = \dfrac{{a\sqrt 3 }}{2}.$

Đáp án : C

Phương pháp giải :

Lời giải chi tiết :

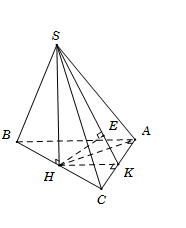Gọi $H$ là trung điểm của $BC,$ suy ra $SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)$.

Gọi $K$ là trung điểm $AC$, suy ra $HK \bot AC$.

Kẻ $HE \bot SK\,\,\,\,\left( {E \in SK} \right).\,\,\,\,\,\,\,\,\left( 1 \right)$

Ta có:$\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot HE\,\,\,\,\left( 2 \right)$

Từ (1) và (2) $ \Rightarrow HE \bot \left( {SAC} \right) \Rightarrow HE = d\left( {H;\left( {SAC} \right)} \right)$

Ta có :

$BH \cap \left( {SAC} \right) = C \Rightarrow \dfrac{{d\left( {B;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{BC}}{{HC}} = 2 \Rightarrow d\left( {B;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HE$

Tam giác $ABC$ vuông tại $A$ nên $BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + 3{a^2}} = 2a$

Tam giác $SBC$ đều cạnh $2a$ nên đường cao $SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 $

Lại có $HK$ là đường trung bình của tam giác $ABC$ nên $HK = \dfrac{1}{2}AB = \dfrac{a}{2}$

Vậy $d\left( {B;\left( {SAC} \right)} \right) = 2HE = \dfrac{{SH.HK}}{{\sqrt {S{H^2} + H{K^2}} }} = \dfrac{{2a\sqrt {39} }}{{13}}.$

Câu 16 :

Cho tứ diện $ABCD$ có $AB \bot CD$ và $AC \bot BD$. Gọi $H$ là hình chiếu vuông góc của $A$ lên $mp(BCD)$. Các khẳng định sau, khẳng định nào sai?

A

$H$ là trực tâm tam giác $BCD$.
B

$CD \bot (ABH)$.
C

$AD \bot BC$.
D

Các khẳng định trên đều sai.

Đáp án : D

Lời giải chi tiết :

Ta có $\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH$. Tương tự $BD \bot CH$

Suy ra $H$ là trực tâm $\Delta BCD$. Suy ra đáp án A, B đúng.

Ta có $\left\{ \begin{array}{l}BC \bot AH\\BC \bot DH\end{array} \right. \Rightarrow BC \bot AD$, suy ra C đúng.

Câu 17 :

A

$\cot \varphi = \dfrac{5}{{\sqrt {15} }}.$
B

$\cot \varphi = \dfrac{{\sqrt {15} }}{5}.$
C

$\varphi = {30^0}.$
D

$\cot \varphi = \dfrac{{\sqrt 3 }}{2}.$

Đáp án : A

Phương pháp giải :

Xác định góc giữa đường thẳng và mặt phẳng (khác ${90^0}$) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

Lời giải chi tiết :

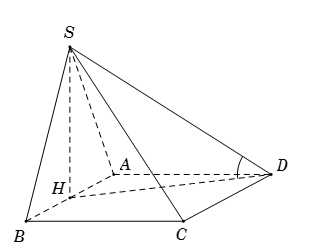Gọi $H$ là trung điểm $AB$, suy ra $SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right).$ Vì $SH \bot \left( {ABCD} \right)$ nên hình chiếu vuông góc của $SD$ trên mặt đáy $\left( {ABCD} \right)$ là $HD$.

Do đó $\widehat {SD,\left( {ABCD} \right)} = \widehat {\left( {SD,HD} \right)} = \widehat {SDH}.$

Tam giác $SAB$ đều cạnh $a$ nên $SH = \dfrac{{a\sqrt 3 }}{2}.$

$HD = \sqrt {A{H^2} + A{B^2}} = \dfrac{{a\sqrt 5 }}{2}.$

Tam giác vuông $SHD$, có $\cot \widehat {SDH} = \dfrac{{DH}}{{SH}} = \dfrac{5}{{\sqrt {15} }}.$

Câu 18 :

A

$S = 2{a^2}.$
B

$S = 2{x^2}.$
C

$S = \dfrac{{\sqrt 3 }}{2}{\left( {a - x} \right)^2}.$
D

$S = 2{\left( {a - x} \right)^2}.$

Đáp án : B

Phương pháp giải :

Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác

Lời giải chi tiết :

Vì S.ABC là hình chóp đều nên $SO \bot \left( {ABC} \right)$ ( với O là tâm của tam giác ABC).

Do đó $SO \bot AO$ mà $\left( \alpha \right) \bot AO$ suy ra $SO\parallel \left( \alpha \right)$.

Tương tự ta cũng có $BC\parallel \left( \alpha \right)$.

Qua M kẻ $IJ\parallel BC$ với $I \in AB,{\rm{ }}J \in AC$; kẻ $MK\parallel SO$ với $K \in SA.$

Khi đó thiết diện là tam giác KIJ.

Diện tích tam giác KIJ là ${S_{\Delta IJK}} = \dfrac{1}{2}IJ.MK$.

Trong tam giác ABC, ta có $\dfrac{{IJ}}{{BC}} = \dfrac{{AM}}{{AA'}}$ (A’ là trung điểm của BC) suy ra $IJ = \dfrac{{AM.BC}}{{AA'}} = \dfrac{{x.a}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2x\sqrt 3 }}{3}$.

Tương tự trong tam giác SAO, ta có $\dfrac{{MK}}{{SO}} = \dfrac{{AM}}{{AO}}$ suy ra $MK = \dfrac{{AM.SO}}{{AO}} = \dfrac{{x.2a}}{{\dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2}}} = 2x\sqrt 3 $.

Vậy ${S_{\Delta IJK}} = \dfrac{1}{2}\dfrac{{2x\sqrt 3 }}{3}.2x\sqrt 3 = 2{x^2}$.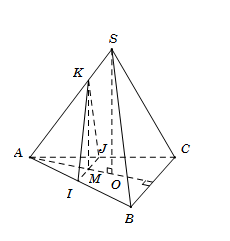

Câu 19 :

A

$45,2^\circ $.
B

$38,1^\circ $.
C

$53,4^\circ $.
D

$61,6^\circ $.

Đáp án : D

Phương pháp giải :

- Xác định giao tuyến của hai mặt phẳng.

- Xác định các đường thẳng lần lượt thuộc hai mặt phẳng mà vuông góc với giao tuyến.

- Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng trên.

- Tính toán dựa vào các kiến thức đã biết ở lớp dưới.

Lời giải chi tiết :

Cách 1: Hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ có giao tuyến là $EF$ như hình vẽ. Từ $A'$ và $D'$ ta kẻ 2 đoạn vuông góc lên giao tuyến $EF$ sẽ là chung một điểm $H$ như hình vẽ. Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng $A'H$ và $D'H$.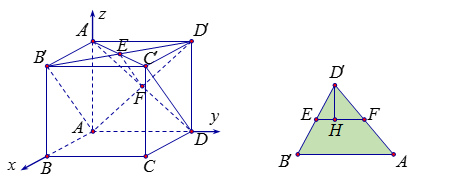

Tam giác $DEF$ lần lượt có $D'E = \dfrac{{D'B'}}{2} = \dfrac{{\sqrt {13} }}{2}$, $D'F = \dfrac{{D'A}}{2} = \dfrac{5}{2}$, $EF = \dfrac{{B'A}}{2} = \sqrt 5 $.

Theo hê rông ta có: ${S_{DEF}} = \dfrac{{\sqrt {61} }}{4}$. Suy ra $D'H = \dfrac{{2{S_{DEF}}}}{{EF}} = \dfrac{{\sqrt {305} }}{{10}}$.

Tam giác $D'A'H$ có: $\cos \widehat {A'HD'} = \dfrac{{H{{A'}^2} + H{{D'}^2} - A'{{D'}^2}}}{{2HA'.HD'}} = - \dfrac{{29}}{{61}}$.

Do đó $\widehat {A'HD'} \approx 118,4^\circ $ hay $\left( {\widehat {A'H,D'H}} \right) \approx 180^\circ - 118,4^\circ = 61,6^\circ $.

Câu 20 :

Cho hình chóp $S.ABC$ trong đó $SA$, $AB$, $BC$ vuông góc với nhau từng đôi một. Biết $SA = 3a$, $AB = a\sqrt 3 $, $BC = a\sqrt 6 $. Khoảng cách từ $B$ đến $SC$ bằng

A

$a\sqrt 2 $.
B

$2a$.
C

$2a\sqrt 3 $.
D

$a\sqrt 3 $.

Đáp án : B

Phương pháp giải :

- Chứng minh $SB \bot CB$.

- Kẻ $BH \bot SC$ và tính độ dài $BH$.

Lời giải chi tiết :

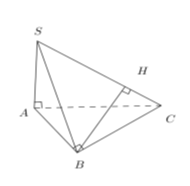Vì $SA,AB,BC$ vuông góc với nhau từng đôi một nên $CB \bot SB$.

Kẻ $BH \bot SC$, khi đó $d\left( {B;SC} \right) = BH$.

Ta có: $SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {9{a^2} + 3{a^2}} = 2\sqrt 3 a$.

Trong tam giác vuông $SBC$ ta có:

$\dfrac{1}{{B{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{C^2}}} \Rightarrow BH = \dfrac{{SB.BC}}{{\sqrt {S{B^2} + B{C^2}} }} = 2a$.

Câu 21 :

Cho hình lập phương ABCD. A’B’C’D’ có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB’D’) và (BC’D) bằng:

A

$\dfrac{{\sqrt 3 }}{3}$
B

$\dfrac{2}{{\sqrt 3 }}$
C

$\dfrac{{\sqrt 3 }}{2}$
D

$\sqrt 3 $

Đáp án : B

Phương pháp giải :

Tính khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ 1 điểm bất kì trên mặt phẳng này đến mặt phẳng kia.

Lời giải chi tiết :

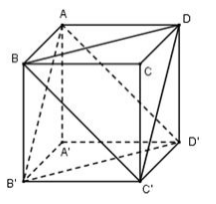Dễ thấy BD // B’D’, BC’ // AD’ nên (AB’D’) // (BC’D)

$ \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3{V_{C'.AB'D'}}}}{{{S_{AB'D'}}}}$

Ta có :

$\begin{array}{l}{V_{C'.AB'D'}} = {V_{A.B'C'D'}} = \dfrac{1}{3}AA'.{S_{B'C'D'}} = \dfrac{1}{3}AA'.\dfrac{1}{2}B'C'.C'D'\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{6}{.2^3} = \dfrac{4}{3}\end{array}$

Tam giác AB’D’ có $AB' = AD' = B'D' = 2\sqrt 2 \Rightarrow \Delta AB'D'$ là tam giác đều cạnh

$2\sqrt 2 \Rightarrow {S_{AB'D'}} = \dfrac{{{{\left( {2\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = 2\sqrt 3 $

Vậy $d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3.\dfrac{4}{3}}}{{2\sqrt 3 }} = \dfrac{2}{{\sqrt 3 }} \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = \dfrac{2}{{\sqrt 3 }}$.

Câu 22 :

A

$d = a\sqrt 3 .$
B

$d = 5a\sqrt 3 .$
C

$d = \dfrac{{5a}}{2}.$
D

$d = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.$

Đáp án : D

Phương pháp giải :

Lời giải chi tiết :

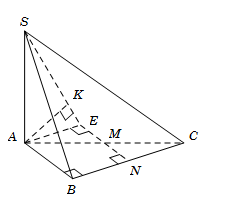Ta có: $AC = \sqrt {A{B^2} + B{C^2}} = 5a$

Xác định ${60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}$ và $SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .$

Gọi $N$ là trung điểm $BC$, suy ra $MN\parallel AB$.

Lấy điểm $E$ đối xứng với $N$ qua $M$, suy ra $ABNE$ là hình chữ nhật.

Do đó $d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).$

Kẻ $AK \bot SE$.

Vì $ME \bot AE,ME \bot SA$ nên $ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK$

Mà $AK \bot SE$ nên $AK \bot \left( {SME} \right)$

Khi đó $d\left( {A;\left( {SME} \right)} \right) = AK = \dfrac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}.$

Câu 23 :

A

$1.$
B

$\sqrt 2 .$
C

$2.$
D

$4.$

Đáp án : C

Phương pháp giải :

Lời giải chi tiết :

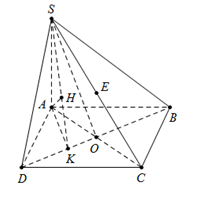Ta có $E \in SC$, $EC \cap \left( {SBD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {C;\left( {SBD} \right)} \right)}} = \dfrac{{d\left( {E;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}$

Từ A kẻ $ AK \bot BD\left( {K \in BD} \right)$, kẻ $AH \bot SK\,\,\left( {H \in SK} \right)\,\,\,\,\,\,\left( 1 \right)$.

Ta có: $\left\{ \begin{array}{l}BD \bot AK\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAK} \right) \Rightarrow BD \bot AH\,\,\,\,\left( 2 \right)$

Từ (1) và (2) $ \Rightarrow AH \bot \left( {SBD} \right).$

$ \Rightarrow AH = d\left( {A;\left( {SBD} \right)} \right) = 2.d\left( {E;\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}.$

Mà $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{K^2}}} \Rightarrow AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} - A{H^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$.

Tam giác $ABD$ vuông tại $A$, có đường cao $AK$.

$ \Rightarrow \dfrac{1}{{A{B^2}}} + \dfrac{1}{{AD{}^2}} = \dfrac{1}{{A{K^2}}} \Leftrightarrow \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}{x^2}}} = \dfrac{5}{{4{a^2}}} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^2} = 4\end{array} \right. \Rightarrow x = 2$

Câu 24 :

A

$\cos \alpha = \dfrac{3}{5}$.
B

$\cos \alpha = \dfrac{{\sqrt 6 }}{3}$.
C

$\cos \alpha = \dfrac{{2\sqrt 2 }}{5}$.
D

$\cos \alpha = \dfrac{{\sqrt {10} }}{5}$.

Đáp án : D

Phương pháp giải :

Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Áp dụng: Tìm hai đường thẳng lần lượt vuông góc với hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBD} \right)$ rồi xác định góc.

Lời giải chi tiết :

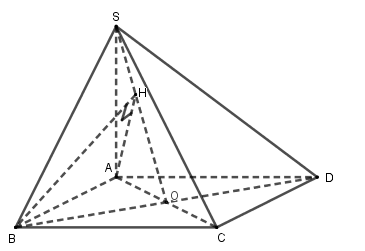Gọi $O$ là tâm hình vuông $ABCD$. Kẻ $AH \bot SO$ tại $H$.

Ta có: $BD \bot AO,$ $BD \bot SA$$ \Rightarrow BD \bot \left( {SAO} \right)$$ \Rightarrow BD \bot AH$. Vậy $AH \bot \left( {SBD} \right)$.

Lại có: $AB \bot \left( {SAD} \right)$, do đó góc $\alpha $ giữa hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBD} \right)$ là góc giữa hai đường thẳng $AH$ và $AB$. Do đó $\alpha = \widehat {BAH}$ và $\widehat {BAH} < {90^0} = \widehat {BHA}$.

Tam giác $SAO$ vuông tại $A$, đường cao $AH$ nên: $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{O^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{4}{{2{a^2}}} = \dfrac{5}{{2{a^2}}}$

Suy ra: $AH = \dfrac{{a\sqrt {10} }}{5}$. Từ đó: $\cos \alpha = \dfrac{{AH}}{{AB}} = \dfrac{{\sqrt {10} }}{5}$.

Câu 25 :

A

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{7}.$
B

${S_{AMIN}} = \dfrac{{12{a^2}\sqrt 6 }}{{35}}.$
C

${S_{AMIN}} = \dfrac{{6{a^2}\sqrt 6 }}{{35}}.$
D

${S_{AMIN}} = \dfrac{{{a^2}\sqrt 6 }}{5}.$

Đáp án : B

Phương pháp giải :

Lời giải chi tiết :

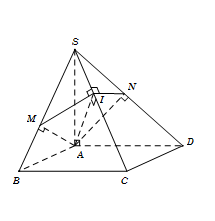Trong tam giác $SAC, $ kẻ $AI \bot SC$ $\left( {\,I \in SC} \right)$

Trong $mp(SBC),$ kẻ ${d_1}$ đi qua $I$ vuông góc với $SC$ cắt $SB $ tại $M.$

Trong $mp(SCD),$ kẻ ${d_2}$ đi qua $I$ vuông góc với $SC$ cắt $SD$ tại $N.$

Khi đó thiết diện của hình chóp cắt bởi mp $\left( \alpha \right)$ là tứ giác $AMIN.$

Ta có $SC \bot \left( \alpha \right) \Rightarrow SC \bot AM$. (1)

Lại có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM$. (2)

Từ (1) và (2), suy ra $AM \bot \left( {SBC} \right) \Rightarrow AM \bot MI$. Chứng minh tương tự, ta được $AN \bot NI$.

Do đó ${S_{AMIN}} = {S_{\Delta AMI}} + {S_{\Delta ANI}} $ $= \dfrac{1}{2}AM.MI + \dfrac{1}{2}AN.NI$.

Vì $AM, AI, AN $ là các đường cao của các tam giác vuông $SAB, SAC, SAD $ nên

$AM = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$; $AI = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = a\sqrt 2 $; $AN = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{2a\sqrt {21} }}{7}$

Suy ra $MI = \sqrt {A{I^2} - A{M^2}} = \dfrac{{a\sqrt {30} }}{5}$ và $NI = \sqrt {A{I^2} - A{N^2}} = \dfrac{{a\sqrt {14} }}{7}$

Vậy ${S_{AMIN}} = \dfrac{1}{2}\left( {\dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{a\sqrt {30} }}{5} + \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{a\sqrt {14} }}{7}} \right) = \dfrac{{12{a^2}\sqrt 6 }}{{35}}$

Bài liên quan