Đề kiểm tra 1 tiết Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 1Đề bài
Câu 1 :
Cho các mệnh đề sau: a. Nếu $a // (P)$ thì $a$ song song với mọi đường thẳng nằm trong $(P).$ b. Nếu $a // (P)$ thì $a$ song song với một đường thẳng nào đó nằm trong $(P).$ c. Nếu $a // (P)$ thì có vô số đường thẳng nằm trong $(P)$ và song song với $a$ d. Nếu $a // (P)$ thì có một đường thẳng $d$ nào đó nằm trong $(P)$ sao cho $a$ và $d$ đồng phẳng. Số mệnh đề đúng là:
Câu 2 :
Cho $2$ đường thẳng \(a,b\) cắt nhau và không đi qua điểm \(A\). Xác định được nhiều nhất bao nhiêu mặt phẳng bởi $a,b$ và $A$?
Câu 3 :
Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A,B,C,D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?
Câu 4 :
Nếu một đường thẳng \(d\) không nằm trong mặt phẳng \(\left( \alpha \right)\) mà nó song song với đường thẳng \(d'\) trong \(\left( \alpha \right)\) thì:
Câu 5 :
Cho hình chóp $S.ABCD$ , đáy là hình thang, đáy lớn $AB$ , Gọi $O$ là giao của $AC$ với $BD$ . $M$ là trung điểm $SC$ . Giao điểm của đường thẳng $AM$ và $mp\left( {SBD} \right)$ là:
Câu 6 :
Cho tứ diện \(ABCD\). Chọn kết luận đúng:
Câu 7 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Câu 8 :
Hai đường thẳng song song thì
Câu 9 :
Hai đường thẳng được gọi là song song nếu:
Câu 10 :
Cho một đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(\left( P \right)\)?
Câu 11 :
Cho hình lập phương $ABCD.A'B'C'D',AC$ và $BD$ cắt nhau tại $O,A'C'$ và $B'D'$ cắt nhau tại $O'$ . Các điểm $M,N,P$ theo thứ tự là trung điểm của $AB,BC,O'B'$. Khi đó thiết diện do mặt phẳng $\left( {MNP} \right)$ cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
Câu 12 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
Câu 13 :
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:
Câu 14 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Tìm giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Câu 15 :
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
Câu 16 :
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
Câu 17 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là một tứ giác ($AB$ không song song với $CD$). Gọi $M$ là trung điểm của $SD, N$ là điểm nằm trên cạnh $SB$ sao cho $SN = 2NB,$ $O$ là giao điểm của $AC$ và $BD.$ Giao điểm của $MN$ với $(ABCD) $ là điểm $K.$ Hãy chọn cách xác định điểm $K$ đúng nhất trong bốn phương án sau:
Câu 18 :
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
Câu 19 :
Cho tứ diện đều $SABC.$ Gọi $I$ là trung điểm của $AB, M $ là một điểm di động trên đoạn $AI.$ Gọi $(P)$ là mặt phẳng qua $M$ và song song với $SI, IC,$ biết $AM = x.$ Thiết diện tạo bởi $mp(P)$ và tứ diện $SABC $ có chu vi là:
Câu 20 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Câu 21 :
Cho hình chóp $S.ABCD,O$ là điểm nằm bên trong tam giác $ACD$. Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) đi qua $O$ và song song với $AC$ và $SD$ có số cạnh bằng:
Câu 22 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = \dfrac{{NC}}{2}\), P là điểm thuộc đoạn CD sao cho \(PD = \dfrac{{PC}}{2}\) . Khi đó mệnh đề nào sau đây là đúng?
Câu 23 :
Cho tứ diện $ABCD,$ $M$ là trung điểm của cạnh $CD,$ $G$ là trọng tâm tứ diện. Khi đó 2 đường thẳng $AD$ và $GM $ là hai đường thẳng:
Câu 24 :
Cho tứ diện $ABCD$ có $AB = CD = a,BC = AD = b,AC = BD = c$. Mặt phẳng \(\left( \alpha \right)\) song song với $AB$ và $CD$ cắt các cạnh của tứ diện theo một thiết diện là hình thoi. Diện tích thiết diện là:
Câu 25 :
Cho hình chóp $S.ABCD $ có $M, N$ lần lượt nằm trên các cạnh $SC, BC.$ Gọi $P$ là giao điểm của $SD$ với mặt phẳng $(AMN).$ $L$ là giao $AN$ và $BD.$ $K$ là giao $AM$ và $LP.$ Khẳng định nào sau đây đúng?
Lời giải và đáp án
Câu 1 :
Cho các mệnh đề sau: a. Nếu $a // (P)$ thì $a$ song song với mọi đường thẳng nằm trong $(P).$ b. Nếu $a // (P)$ thì $a$ song song với một đường thẳng nào đó nằm trong $(P).$ c. Nếu $a // (P)$ thì có vô số đường thẳng nằm trong $(P)$ và song song với $a$ d. Nếu $a // (P)$ thì có một đường thẳng $d$ nào đó nằm trong $(P)$ sao cho $a$ và $d$ đồng phẳng. Số mệnh đề đúng là:
Đáp án : C Phương pháp giải :
Vận dụng các kiến thức về đường thẳng song song với mặt phẳng. Lời giải chi tiết :
Các mệnh đề b, c, d đúng nên có $3$ mệnh đề đúng.
Câu 2 :
Cho $2$ đường thẳng \(a,b\) cắt nhau và không đi qua điểm \(A\). Xác định được nhiều nhất bao nhiêu mặt phẳng bởi $a,b$ và $A$?
Đáp án : C Lời giải chi tiết :
Có $3$ mặt phẳng gồm \(\left( {a,b} \right),\left( {A,a} \right),\left( {A,b} \right)\).
Câu 3 :
Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A,B,C,D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?
Đáp án : C Phương pháp giải :
Sử dụng điều kiện xác định mặt phẳng: Qua ba điểm không thẳng hàng, xác định duy nhất một mặt phẳng. Lời giải chi tiết :
Điểm \(S\) cùng với hai trong số bốn điểm \(A,B,C,D\) tạo thành một mặt phẳng, từ bốn điểm ta có $6$ cách chọn ra hai điểm, nên có tất cả $6$ mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên.
Câu 4 :
Nếu một đường thẳng \(d\) không nằm trong mặt phẳng \(\left( \alpha \right)\) mà nó song song với đường thẳng \(d'\) trong \(\left( \alpha \right)\) thì:
Đáp án : A Lời giải chi tiết :
Nếu đường thẳng \(d\) không nằm trong mặt phẳng \(\left( \alpha \right)\) mà \(d\) song song với một đường thẳng \(d'\) nằm trong \(\left( \alpha \right)\) thì \(d\) song song với \(\left( \alpha \right)\).
Câu 5 :
Cho hình chóp $S.ABCD$ , đáy là hình thang, đáy lớn $AB$ , Gọi $O$ là giao của $AC$ với $BD$ . $M$ là trung điểm $SC$ . Giao điểm của đường thẳng $AM$ và $mp\left( {SBD} \right)$ là:
Đáp án : A Phương pháp giải :
Đưa về cùng mặt phẳng, tìm trong mặt phẳng $\left( {SBD} \right)$ một đường thẳng đồng phẳng với $AM$ . Lời giải chi tiết :
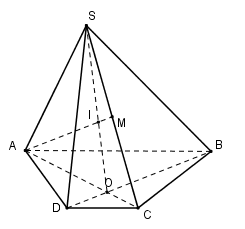 Xét trong $\left( {SAC} \right)$ ta gọi \(I = AM \cap SO,SO \subset \left( {SBD} \right) \) \(\Rightarrow AM \cap \left( {SBD} \right) = I\)
Câu 6 :
Cho tứ diện \(ABCD\). Chọn kết luận đúng:
Đáp án : C Phương pháp giải :
Vẽ hình và xét vị trí tương đối của đường thẳng và mặt phẳng. Lời giải chi tiết :
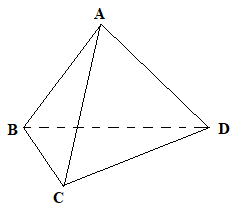 Từ hình vẽ ta thấy: +) Đường thẳng \(AD\) cắt mặt phẳng \(\left( {ABC} \right)\) tại điểm duy nhất \(A\) nên đáp án A, B đều sai. +) \(A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng. +) Đường thẳng \(AC\) cắt mặt phẳng \(\left( {ABD} \right)\) tại điểm duy nhất \(A\) nên D sai.
Câu 7 :
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án : A Lời giải chi tiết :
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau thì mọi đường thẳng nằm trong \(\left( \alpha \right)\) đều song song với \(\left( \beta \right)\).
Câu 8 :
Hai đường thẳng song song thì
Đáp án : C Lời giải chi tiết :
Hai đường thẳng song song với nhau thì chúng đồng phẳng và không có điểm chung.
Câu 9 :
Hai đường thẳng được gọi là song song nếu:
Đáp án : D Lời giải chi tiết :
Hai đường thẳng được gọi là song song nếu chúng đồng phẳng và không có điểm chung.
Câu 10 :
Cho một đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(\left( P \right)\)?
Đáp án : B Lời giải chi tiết :
Nếu đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) thì có duy nhất một mặt phẳng chứa \(a\) và song song với \(\left( P \right)\).
Câu 11 :
Cho hình lập phương $ABCD.A'B'C'D',AC$ và $BD$ cắt nhau tại $O,A'C'$ và $B'D'$ cắt nhau tại $O'$ . Các điểm $M,N,P$ theo thứ tự là trung điểm của $AB,BC,O'B'$. Khi đó thiết diện do mặt phẳng $\left( {MNP} \right)$ cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?
Đáp án : B Phương pháp giải :
Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung $M$ và lần lượt chứa hai đường thẳng song song $d$ và $d'$ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua $M$ và song song với $d$ và $d'$. Lời giải chi tiết :
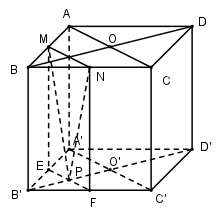 Ta có: $MN$ là đường trung bình của tam giác $ABC$ nên $MN//AC//A'C'$ . $\left( {MNP} \right)$ và $\left( {A'B'C'D'} \right)$ có điểm $P$ chung và $MN//A'C'$ . Qua $P$ kẻ \(EF//A'C';E \in A'B',F \in B'C'.\) Vậy thiết diện của hình lập phương cắt bởi $mp\left( {MNP} \right)$ là $MNFE$.
Câu 12 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
Đáp án : B Phương pháp giải :
\(\left\{ \begin{array}{l}a//\left( \beta \right)\\b//\left( \beta \right)\\a \cap b \subset \left( \alpha \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) hoặc \(\left\{ \begin{array}{l}a//a'\\b//b'\\a \cap b \subset \left( \alpha \right)\\a',b' \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) Lời giải chi tiết :
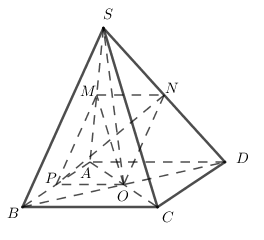 Dễ dàng chứng minh được $MNOP $ là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai. Ta có : $MN$ là đường trung bình của tam giác $SAD$ \( \Rightarrow MN//AD//BC\) $ON$ là đường trung bình của tam giác $SBD$ \( \Rightarrow ON//SB\) \( \Rightarrow (MON) // (SBC)\) \( \Rightarrow \) Đáp án B đúng. Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\)
Câu 13 :
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:
Đáp án : D Phương pháp giải :
Đưa về cùng mặt phẳng và vận dụng các kiến thức hình học phẳng Lời giải chi tiết :
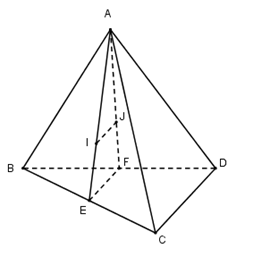 Gọi $E, F$ lần lượt là trung điểm của $BC$ và $BD$ ta có: $\begin{array}{l}I \in AE\,;\,\dfrac{{AI}}{{AE}} = \dfrac{2}{3}\\J \in AF\,;\,\dfrac{{AJ}}{{AF}} = \dfrac{2}{3}\end{array}$ Xét trong $mp(AEF)$ ta suy ra \(IJ//EF\) (Định lí Ta – let đảo) Mà $EF$ là đường trung bình của tam giác $ABC$ \( \Rightarrow \) $EF // CD$ Vậy $IJ // CD.$
Câu 14 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Tìm giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Đáp án : B Phương pháp giải :
- Tìm giao điểm dễ thấy của hai mặt phẳng. - Tìm giao điểm thứ hai bằng cách tìm hai đường thẳng nằm trong hai mặt phẳng mà chúng cắt nhau. Lời giải chi tiết :
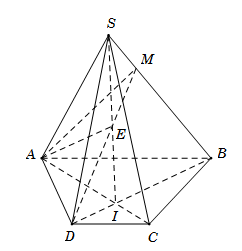 Ta có \(A\) là điểm chung thứ nhất của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\). Trong mặt phẳng \(\left( {SBD} \right)\), gọi \(E = SI \cap DM\). Ta có: ● \(E \in SI\) mà \(SI \subset \left( {SAC} \right)\) suy ra \(E \in \left( {SAC} \right)\). ● \(E \in DM\) mà \(DM \subset \left( {ADM} \right)\) suy ra \(E \in \left( {ADM} \right)\). Do đó \(E\) là điểm chung thứ hai của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\). Vậy $AE$ là giao tuyến của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Câu 15 :
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
Đáp án : B Phương pháp giải :
Để chứng minh ba đường thẳng \({d_1},{\rm{ }}{d_2},{\rm{ }}{d_3}\) đồng quy ta chứng minh giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\) là điểm chung của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\); đồng thời \({d_3}\) là giao tuyến \(\left( \alpha \right)\) và \(\left( \beta \right)\). Lời giải chi tiết :
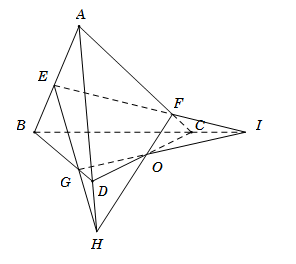 Trong $mp(EHI)$, gọi \(O = HF \cap IG\). Ta có ● \(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\). ● \(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\). Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\) Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\). Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
Câu 16 :
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
Đáp án : A Phương pháp giải :
- Sử dụng các tính chất của trọng tâm tam giác. - Sử dụng tính chất đường trung bình của tam giác. - Sử dụng định nghĩa hai đường thẳng song song. Lời giải chi tiết :
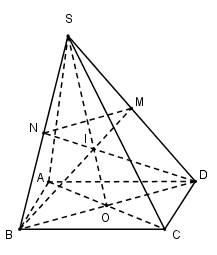 Dễ thấy $I$ là trọng tâm của tam giác $SBD $ nên $BI, DI$ là các đường trung tuyến của tam giác $SBD.$ Suy ra $M, N$ lần lượt là trung điểm của $SD$ và $SB.$ Nên $MN$ là đường trung bình của tam giác $SBD$ \( \Rightarrow \) $MN // BD.$ Vậy tứ giác $MNBD $ là hình thang.
Câu 17 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là một tứ giác ($AB$ không song song với $CD$). Gọi $M$ là trung điểm của $SD, N$ là điểm nằm trên cạnh $SB$ sao cho $SN = 2NB,$ $O$ là giao điểm của $AC$ và $BD.$ Giao điểm của $MN$ với $(ABCD) $ là điểm $K.$ Hãy chọn cách xác định điểm $K$ đúng nhất trong bốn phương án sau:
Đáp án : D Phương pháp giải :
Đưa về cùng mặt phẳng. Xác định giao tuyến của mặt phẳng và đường bằng cách xác định điểm chung của đường thẳng này và một đường thẳng khác nằm trong mặt phẳng kia. Lời giải chi tiết :
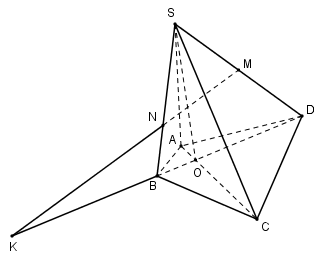 Ta có: \(\dfrac{{SM}}{{SD}} \ne \dfrac{{SN}}{{SB}} \Rightarrow \) $MN$ và $BD$ không song song. Trong $(SBD) $ gọi \(K = MN \cap BD \Rightarrow K \in BD \subset \left( {ABCD} \right) \Rightarrow K = MN \cap \left( {ABCD} \right).\)
Câu 18 :
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
Đáp án : B Phương pháp giải :
Đừa về cùng mặt phẳng. Tìm trong mặt phẳng $(SAB)$ một đường thẳng cắt $DY.$ Giao điểm của đường thẳng đó và $SO$ chính là giao điểm của $(SAB)$ và $DY.$ Lời giải chi tiết :
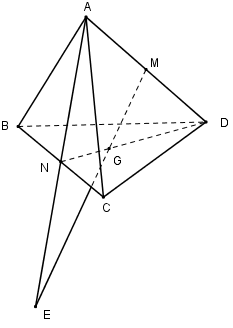 Ta có: \(\dfrac{{DM}}{{DA}} \ne \dfrac{{DG}}{{DN}}\,\,\left( {\dfrac{1}{2} \ne \dfrac{2}{3}} \right) \) \(\Rightarrow \) $MG$ và $AN$ không song song với nhau. Trong $(ADN)$ gọi \(E = MG \cap AN.\) Mà \(AN \subset \left( {ABC} \right) \Rightarrow MG \cap \left( {ABC} \right) = E.\)
Câu 19 :
Cho tứ diện đều $SABC.$ Gọi $I$ là trung điểm của $AB, M $ là một điểm di động trên đoạn $AI.$ Gọi $(P)$ là mặt phẳng qua $M$ và song song với $SI, IC,$ biết $AM = x.$ Thiết diện tạo bởi $mp(P)$ và tứ diện $SABC $ có chu vi là:
Đáp án : B Phương pháp giải :
- Đưa về cùng mặt phẳng. - Sử dụng tính chất của đường thẳng song song với mặt phẳng. - Áp dụng định lí Ta-let đảo để chỉ ra các tỉ lệ bằng nhau. - Công thức tính chu vi tam giác. Lời giải chi tiết :
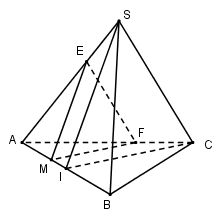 Trong $mp(ABC)$ kẻ $MF // IC$ \(\left( {F \in AC} \right)\), trong $mp(SAB)$ kẻ $ME // SI$ \(\left( {E \in SA} \right)\). Do đó $mp(P)$ chính là $(MEF)$ và thiết diện tạo bởi $mp(P)$ và tứ diện đều $SABC$ là tam giác $MEF.$ Gọi $a$ là cạnh của tứ diện đều $SABC.$ Xét tam giác đều $ABC$ và tam giác $SAB$ là những tam giác đều cạnh $a$ nên \(CI = SI = \dfrac{{a\sqrt 3 }}{2}\). Trong $(ABC)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{ME}}{{SI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{ME}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow ME = x\sqrt 3 .\) Trong $(SAB)$ ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{MF}}{{CI}} \Leftrightarrow \dfrac{x}{{\dfrac{a}{2}}} = \dfrac{{MF}}{{\dfrac{{a\sqrt 3 }}{2}}} \Leftrightarrow MF = x\sqrt 3 .\) Ta lại có: \(\dfrac{{AM}}{{AI}} = \dfrac{{AF}}{{AC}} = \dfrac{{AE}}{{AS}} \) \(\Rightarrow EF\) $// SC $ (Định lí Ta-let đảo) \( \Rightarrow \dfrac{{EF}}{{SC}} = \dfrac{{AF}}{{AC}} = \dfrac{{AM}}{{AI}} \Leftrightarrow \dfrac{{EF}}{a} = \dfrac{x}{{\dfrac{a}{2}}} \Leftrightarrow EF = 2x\) Vậy chu vi tam giác $MEF $ bằng $ME + MF + EF =$ \(x\sqrt 3 + x\sqrt 3 + 2x = 2x\left( {1 + \sqrt 3 } \right)\)
Câu 20 :
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Đáp án : C Phương pháp giải :
- Tính chất đường thẳng song song với mặt phẳng. - Định lí đường trung bình của tam giác. Lời giải chi tiết :
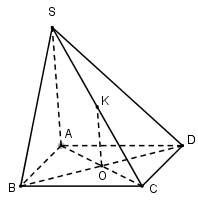 Gọi $O$ là giao điểm của $AC$ và $BD$ Trong mặt phẳng $SAC,$ qua $O$ kẻ ${\rm{O}}K \bot AC\,\,\left( {K \in SC} \right)$, suy ra $mp$\(\left( \alpha \right)\) chính là $mp(BDK).$ $OK // SA ; AO = OC$\( \Rightarrow \) $SK = KC.$ (Định lí đường trung bình của tam giác)
Câu 21 :
Cho hình chóp $S.ABCD,O$ là điểm nằm bên trong tam giác $ACD$. Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) đi qua $O$ và song song với $AC$ và $SD$ có số cạnh bằng:
Đáp án : C Phương pháp giải :
- Từ những giả thiết ban đầu xác định \(mp\left( \alpha \right)\). - Dựng thiết diện của \(mp\left( \alpha \right)\) với hình chóp. Lời giải chi tiết :
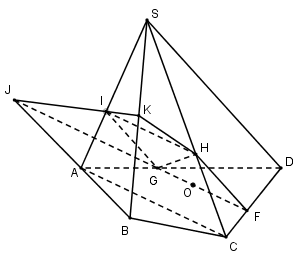 Trong $\left( {ABCD} \right)$ qua $O$ kẻ \(GF//AC\left( {G \in AD,F \in CD} \right)\) Trong $\left( {SCD} \right)$ qua $F$ kẻ \(FH//SD\left( {H \in SC} \right)\) \( \Rightarrow \left( \alpha \right)\) là $\left( {GFH} \right)$ . \(\left( \alpha \right) \cap \left( {ABCD} \right) = GF,\left( \alpha \right) \cap \left( {SCD} \right) = HF.\) Ta có: \(\left( \alpha \right)\) và $\left( {SAC} \right)$ có $H$ chung, \(\left( \alpha \right) \supset GF,\left( {SAC} \right) \supset AC,GF//AC\). \( \Rightarrow \) Qua $H$ kẻ \(HI//AC\left( {I \in SA} \right)\) \( \Rightarrow \left( \alpha \right) \cap \left( {SAC} \right) = HI,\left( \alpha \right) \cap \left( {SAD} \right) = GI\). Trong $\left( {ABCD} \right)$ gọi \(J = GF \cap AB \Rightarrow J \in AB \Rightarrow J \in \left( {SAB} \right)\) Trong $\left( {SAB} \right)$ gọi \(K = IJ \cap SB\left( {K \in SB} \right)\) \( \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = IK,\left( \alpha \right) \cap \left( {SBC} \right) = HK\) Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) là $GFHKI$ là đa giác có $5$ cạnh.
Câu 22 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = \dfrac{{NC}}{2}\), P là điểm thuộc đoạn CD sao cho \(PD = \dfrac{{PC}}{2}\) . Khi đó mệnh đề nào sau đây là đúng?
Đáp án : A Phương pháp giải :
Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia. Lời giải chi tiết :
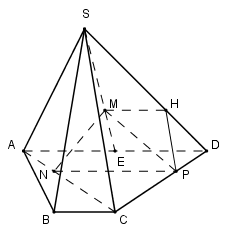 Gọi \(H \in SD\) sao cho \(HD = \dfrac{1}{2}SH\) Ta có: \(\dfrac{{SM}}{{SE}} = \dfrac{{SH}}{{SD}} = \dfrac{2}{3} \Rightarrow MH//AD//NP \Rightarrow M,H,P,N\) đồng phẳng. Ta có: \(\begin{array}{l}\dfrac{{AN}}{{AC}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow NP//AD;\,\,\dfrac{{DH}}{{DS}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow HP//SC\\\left\{ \begin{array}{l}NP//AD//BC\\HP//SC\end{array} \right. \Rightarrow \left( {MHPN} \right)//\left( {SBC} \right) \Rightarrow \left( {MNP} \right)//\left( {SBC} \right)\\MN \subset \left( {MNP} \right) \Rightarrow MN//\left( {SBC} \right)\end{array}\)
Câu 23 :
Cho tứ diện $ABCD,$ $M$ là trung điểm của cạnh $CD,$ $G$ là trọng tâm tứ diện. Khi đó 2 đường thẳng $AD$ và $GM $ là hai đường thẳng:
Đáp án : A Phương pháp giải :
- Định nghĩa hai đường thẳng chéo nhau, hai đường thẳng song song, hai đường thẳng cắt nhau. Lời giải chi tiết :
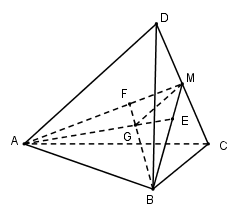 Gọi $M$ là trung điểm của $CD, E$ và $F$ lần lượt là trọng tâm tam giác $BCD$ và $ACD$ \( \Rightarrow E \in BM,F \in AM.\) Trong $(AMB):$ \(G = AE \cap BF \Rightarrow \) $G$ là trọng tâm của tứ diện $ABCD.$ Giả sử bốn điểm $A, D, G, M$ đồng phẳng. $A, D, M$\( \in \left( {ACD} \right)\) \( \Rightarrow G \in \left( {ACD} \right) \) \(\Rightarrow AG \subset \left( {ACD} \right)\) \( \Rightarrow E \in \left( {ACD} \right)\)(Vô lí) Do đó $A, D, M, G $ không đồng phẳng. Vậy $AD $ và $GM$ là hai đường thẳng chéo nhau.
Câu 24 :
Cho tứ diện $ABCD$ có $AB = CD = a,BC = AD = b,AC = BD = c$. Mặt phẳng \(\left( \alpha \right)\) song song với $AB$ và $CD$ cắt các cạnh của tứ diện theo một thiết diện là hình thoi. Diện tích thiết diện là:
Đáp án : D Phương pháp giải :
- Đưa về cùng mặt phẳng. - Sử dụng các yếu tố song song để xác định hình dạng của thiết diện. - Điều kiện để thiết diện trở thành hình thoi. - Công thức tính diện tích hình thoi \(S = \dfrac{1}{2}{d_1}{d_2},\) trong đó \({d_1},{d_2}\) là độ dài hai đường chéo của hình thoi. Lời giải chi tiết :
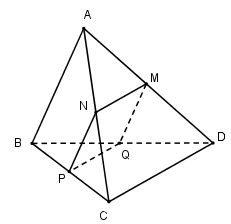 Giả sử \(\left( \alpha \right)\) cắt các cạnh $AD,AC,CB,BD$ theo thứ tự tại $M,N,P,Q$. \(\left\{ \begin{array}{l}CD//\left( \alpha \right),CD \subset \left( {ACD} \right)\\M \in \left( \alpha \right) \cap \left( {ACD} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {ACD} \right) = MN//CD\,\,\left( {N \in AC} \right)\) Tương tự \(\left( \alpha \right) \cap \left( {BCD} \right) = PQ//CD\,\,\left( {Q \in BD} \right).\) Khi đó: \(\left( \alpha \right) \cap \left( {ABD} \right) = MQ//AB,\left( \alpha \right) \cap \left( {ABC} \right) = NP//AB.\) Hình bình hành $MNPQ$ là thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\). Theo định lí Ta-let ta có: \(\dfrac{{NP}}{{AB}} = \dfrac{{CN}}{{CA}} \Rightarrow NP = \dfrac{a}{c}CN,\,\,\dfrac{{MN}}{{CD}} = \dfrac{{AN}}{{AC}} \Rightarrow MN = \dfrac{a}{b}AN.\) Để MNPQ là hình thoi thì \(MN = NP \Rightarrow CN = AN\) hay $N$ là trung điểm của $AC$ . Từ đó suy ra $M,P,Q$ lần lượt là trung điểm của $AD,BC,BD$ . Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}D{N^2} = \dfrac{{A{D^2} + D{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\\B{N^2} = \dfrac{{A{B^2} + B{C^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\\ \Rightarrow DN = BN\end{array}\) \( \Rightarrow \Delta NBD\) cân tại $N$ . Lại có $Q$ là trung điểm của $BD$ nên \(NQ \bot BD.\) Do đó ta có: \(N{Q^2} = N{B^2} - B{Q^2} = \dfrac{{{b^2} + {a^2}}}{2} - \dfrac{{{c^2}}}{4} - \dfrac{{{c^2}}}{4} = \dfrac{{{b^2} + {a^2} - {c^2}}}{2}\) Tương tự ta tính được \(M{P^2} = \dfrac{{{c^2} + {a^2} - {b^2}}}{2}.\) Vậy \({S_{MNPQ}} = \dfrac{1}{2}MP.NQ = \dfrac{1}{2}\sqrt {\dfrac{{{b^2} + {a^2} - {c^2}}}{2}.\dfrac{{{c^2} + {a^2} - {b^2}}}{2}} = \dfrac{1}{4}\sqrt {\left( {{b^2} + {a^2} - {c^2}} \right)\left( {{c^2} + {a^2} - {b^2}} \right)} \) .
Câu 25 :
Cho hình chóp $S.ABCD $ có $M, N$ lần lượt nằm trên các cạnh $SC, BC.$ Gọi $P$ là giao điểm của $SD$ với mặt phẳng $(AMN).$ $L$ là giao $AN$ và $BD.$ $K$ là giao $AM$ và $LP.$ Khẳng định nào sau đây đúng?
Đáp án : C Phương pháp giải :
- Xét tính đúng sai của từng đáp án dựa vào các quan hệ điểm thuộc đường thẳng, điểm thuộc mặt phẳng. - Sử dụng phương pháp tìm giao tuyến của hai mặt phẳng để tìm giao tuyến hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {SBD} \right)\). Lời giải chi tiết :
Vì $L$ là giao của $AN$ và $BD$ nên $L ∈ BD$ $⇒ L ∈ (SBD)$ Có $P ∈ SD ⇒ P ∈ (SBD)$ $ \Rightarrow LP \subset \left( {SBD} \right) \Rightarrow KL \subset \left( {SBD} \right)$ Vì $K ∈ AM; L ∈ AN ⇒ KL ⊂ (AMN)$ Vậy $KL$ là giao tuyến của $(AMN) $ và $(SBD)$ 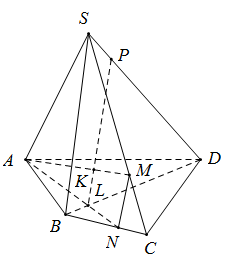 |


















