Câu hỏi:
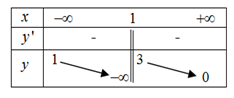
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình bên. Số đường tiệm cận của đồ thị hàm số \(y = f(x)\) là
- A \(1\)
- B \(4\)
- C \(3\)
- D \(2\)
Phương pháp giải:
Sử dụng định nghĩa tiệm cận :
Đường thẳng \(y = {y_0}\) là tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu một trong các điều kiện sau được thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0};\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\)
Đường thẳng \(x = {x_0}\) là tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) nếu một trong các điều kiện sau được thỏa mãn \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết:
Từ bảng biến thiên ta suy ra \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 1;\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\) nên \(y = 0;y = 1\) là các đường tiệm cận ngang của đồ thị hàm số.
Và \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \) nên đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có ba đường tiệm cận.
Chọn C.