Câu hỏi:
Cho hình lập phương \(ABCD.A'B'C'D'\). Hệ thức nào sau đây đúng?
- A \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AA'} \)
- B \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {AA'} \)
- C \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
- D \(\overrightarrow {AC'} = \overrightarrow {BD} + \overrightarrow {AC} + \overrightarrow {AA'} \)
Phương pháp giải:
Sử dụng công thức ba điểm và các vectơ bằng nhau.
Lời giải chi tiết:
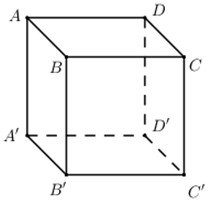
Ta có: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} \).
Mà \(\overrightarrow {BC} = \overrightarrow {AD} ,\,\,\overrightarrow {CC'} = \overrightarrow {AA'} \Rightarrow \overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Chọn C.
Quảng cáo


















