Câu hỏi:
Trong các giới hạn sau đây, giới hạn nào có giá trị bằng \( + \infty \)?
- A \(\lim \dfrac{{2{n^3} + 3}}{{1 - 2{n^2}}}\)
- B \(\lim \left( {{n^3} - 4{n^2} + 1} \right)\)
- C \(\lim \dfrac{{{3^{n + 1}} + 2n}}{{5 + {3^n}}}\)
- D \(\lim \dfrac{{3{n^2} + n}}{{4{n^2} - 5}}\)
Phương pháp giải:
Sử dụng MTCT tính giới hạn ở từng đáp án và kết luận.
Lời giải chi tiết:
Đáp án A: 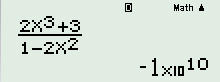
Đáp án B: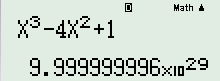
Đáp án C: 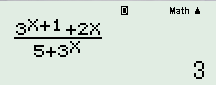
Đáp án D: 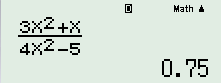
Chọn B.
Quảng cáo


















