Câu hỏi:
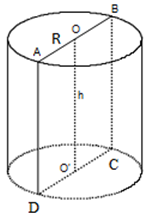
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật \(ABCD\) có \(AB\) và \(CD\) thuộc hai đáy của hình trụ, \(AB = 4a,\,AC = 5a\). Thể tích của khối trụ.
- A \(8\pi {a^3}\).
- B \(12\pi {a^3}\).
- C \(4\pi {a^3}\).
- D \(16\pi {a^3}\).
Phương pháp giải:
Thể tích khối trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết:
ABCD là hình chữ nhật
\( \Rightarrow A{C^2} = A{B^2} + A{D^2} \Leftrightarrow {\left( {5a} \right)^2} = {\left( {4a} \right)^2} + A{D^2} \Leftrightarrow AD = 3a\)
Khối trụ đã cho có chiều cao \(h = AD = 3a\), bán kính đáy \(r = \frac{{AB}}{2} = \frac{{4a}}{2} = 2a\)
Thể tích của khối trụ: \(V = \pi {r^2}h = \pi {\left( {2a} \right)^2}.3a = 12\pi {a^3}\)
Chọn: B
Quảng cáo
Câu hỏi trước
