Phương pháp giải:

Xét hàm số, tìm GTLN.

Lời giải chi tiết:

Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ.

Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = \pi  \Rightarrow h = \dfrac{{1 - 2{R^2}}}{{2R}}\)

Do \(h > 0 \Rightarrow 1 - 2{R^2} > 0 \Leftrightarrow {R^2} < \dfrac{1}{2} \Leftrightarrow 0 < R < \dfrac{{\sqrt 2 }}{2}\).

Thể tích khối trụ: \(V = \pi {R^2}h = \pi {R^2}.\dfrac{{1 - 2{R^2}}}{{2R}} = \dfrac{{\pi \left( {R - 2{R^3}} \right)}}{2}\)

Xét hàm số \(g\left( R \right) = \dfrac{\pi }{2}\left( {R - 2{R^3}} \right)\) trên \(\left( {0;\dfrac{{\sqrt 2 }}{2}} \right)\).

Ta có: \(g'\left( R \right) = \dfrac{\pi }{2}\left( {1 - 6{R^2}} \right),\,\,g'\left( R \right) = 0 \Leftrightarrow R = \dfrac{{\sqrt 6 }}{6}\,\,\left( {Do\,\,R > 0} \right)\)

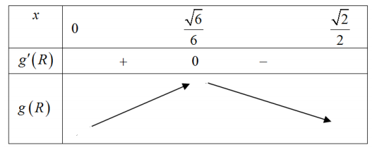
Bảng biến thiên:

Vậy, thể tích khối trụ lớn nhất khi \(R = \dfrac{{\sqrt 6 }}{6} \Rightarrow h = \dfrac{{\sqrt 6 }}{3}\).

Chọn: B