Câu hỏi:
Cho tứ diện ABCD có \(AB = x\) thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.
- A \(\frac{{a\sqrt 3 }}{3}\).
- B \(\frac{{a\sqrt 6 }}{4}\).
- C \(\frac{{a\sqrt 3 }}{4}\).
- D \(\frac{{a\sqrt 6 }}{3}\).
Phương pháp giải:
Lời giải chi tiết:
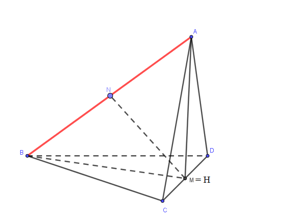
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD))
\( \Rightarrow H \in BM,\,\,AH \bot HM\)
\({V_{ABCD}}\) lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác \(ACD,\,\,BCD\) đều, cạnh a, có đường cao \(AM,\,BM\) bằng \(\frac{{a\sqrt 3 }}{2}\)
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB \( \Rightarrow MN \bot AB\)
Mà \(MN \subset \left( {AMB} \right) \bot CD \Rightarrow MN \bot CD \Rightarrow MN\) là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là : \(MN = \frac{{AM}}{{\sqrt 2 }} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt 2 }} = \frac{{a\sqrt 6 }}{4}\).
Chọn: B