Câu hỏi:
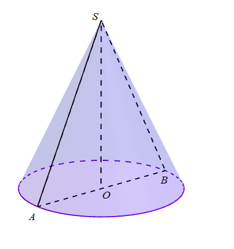
Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8. Khẳng định nào sau đây sai ?
- A Khối nón có diện tích đáy bằng \(8\pi \).
- B Khối nón có diện tích xung quanh bằng \(16\pi \sqrt 2 \).
- C Khối nón có độ dài đường sinh bằng 4.
- D Khối nón có thể tích bằng \(\frac{{16\pi \sqrt 2 }}{3}\).
Phương pháp giải:
Diện tích hình tròn bán kính R: \(S = \pi {R^2}\)
Diện tích xung quanh của khối nón: \({S_{xq}} = \pi Rl\)
Thể tích khối nón: \(V = \frac{1}{3}\pi {R^2}h\).
Lời giải chi tiết:
Theo đề bài, ta có tam giác SAB vuông cân tại S và \({S_{\Delta SAB}} = 8\)
Ta có: \({S_{\Delta SAB}} = \frac{1}{2}.SO.AB = \frac{1}{2}.OA.2OA = O{A^2} = 8 \Rightarrow OA = 2\sqrt 2 \)
\( \Rightarrow \) Đường tròn đáy có bán kính \(R = OA = 2\sqrt 2 \)
Diện tích đáy: \(S = \pi {R^2} = \pi {\left( {2\sqrt 2 } \right)^2} = 8\pi \)
Độ dài đường sinh: \(l = SA = OA.\sqrt 2 = 2\sqrt 2 .\sqrt 2 = 4\)
Diện tích xung quanh của khối nón: \({S_{xq}} = \pi Rl = \pi .2\sqrt 2 .4 = 8\sqrt 2 \pi \)
Đường cao: \(h = SO = OA = 2\sqrt 2 \)
Thể tích khối nón: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}.\pi .{\left( {2\sqrt 2 } \right)^2}.2\sqrt 2 = \frac{{16\sqrt 2 \pi }}{3}\).
Chọn: B