Câu hỏi:
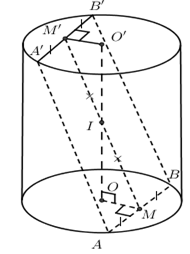
Cho hình trụ có bán kính đáy bằng 4cm. Mặt phẳng (P) không vuông góc với đáy, cắt hai mặt đáy theo dây cung song song với AB và A’B’. AB = A’B’ = 6 cm. Biết \({{S}_{ABB'A'}}=60c{{m}^{2}}.\) Tính chiều cao của hình trụ
- A \(6\sqrt{3}\)
- B \(6\sqrt{2}\)
- C \(6\sqrt{5}\)
- D
\(6\sqrt{7}\)
Phương pháp giải:
Lời giải chi tiết:
+) Vẽ M, M’ lần lượt là trung điểm của AB, A’B’.
+) Nhận xét: ABA’B’ là hình chữ nhật
+) Diện tích hình chữ nhật ABA’B’: \({{S}_{ABA'B'}}=AB.BB'=60\)
\(\Rightarrow BB'=\frac{60}{AB}=\frac{60}{6}=10cm=MM'\Rightarrow IM=\frac{MM'}{2}=5cm\)
+) Trong tam giác vuông OMA: \(OM=\sqrt{O{{A}^{2}}-M{{A}^{2}}}=\sqrt{{{4}^{2}}-{{3}^{2}}}=\sqrt{16-9}=\sqrt{7}\)
\(\Rightarrow OI=\sqrt{I{{M}^{2}}-O{{M}^{2}}}=\sqrt{{{5}^{2}}-7}=\sqrt{25-7}=\sqrt{18}=3\sqrt{2}\)
+) Chiều cao của hình trụ là: \(h=2OI=2.3\sqrt{2}=6\sqrt{2}\,cm\)
Chọn đáp án B
Câu hỏi trước
