Câu hỏi:
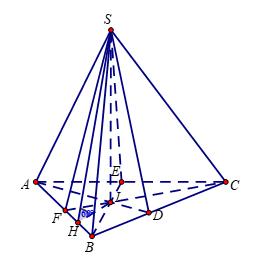
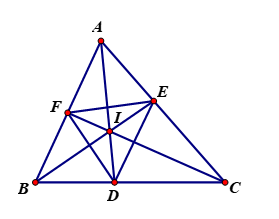
Cho hình chóp \(S.ABC\) có \(AB = 5cm,\;BC = 6cm,\;CA = 7cm\). Hình chiếu vuông góc của \(S\) xuống mặt phẳng \(\left( {ABC} \right)\) nằm bên trong tam giác \(ABC\). Các mặt phẳng \(\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)\) đều tạo với đáy một góc \(60^\circ \). Gọi \(AD,\;BE,\;CF\) là các đường phân giác của tam giác \(ABC\) với \(D \in BC,E \in AC,F \in AB\) .Thể tích \(S.DEF\) gần nhất với số nào sau đây?
- A \(2,9\,c{m^3}\).
- B \(4,1\,\,c{m^3}\).
- C \(3,7\,c{m^3}\).
- D \(3,4\,c{m^3}\).
Phương pháp giải:
Lời giải chi tiết:
Vì các mặt phẳng \(\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)\) đều tạo với đáy một góc \(60^\circ \) và hình chiếu vuông góc của \(S\) xuống mặt phẳng \(\left( {ABC} \right)\) nằm bên trong tam giác \(ABC\) nên ta có hình chiếu của \(S\) xuống mặt phẳng \(\left( {ABC} \right)\) là tâm đường tròn nội tiếp \(I\) của tam giác \(ABC\).
Gọi \(p\) là nửa chu vi tam giác \(ABC\) thì \(p = \frac{{5 + 6 + 7}}{2} = 9\).
Ta có \({S_{ABC}} = \sqrt {9\left( {9 - 5} \right)\left( {9 - 6} \right)\left( {9 - 7} \right)} = 6\sqrt 6 \) và \(r = \frac{S}{p} = \frac{{6\sqrt 6 }}{9} = \frac{{2\sqrt 6 }}{3}\).
Chiều cao của hình chóp là: \(h = r.\tan 60^\circ = 2\sqrt 2 \).
Kí hiệu \(BC = a,AC = b,AB = c\). Ta có:
Vì \(BE\) là phân giác của góc \(B\) nên ta có: \(\frac{{AE}}{{CE}} = \frac{{BA}}{{BC}}\). Tương tự \(\frac{{FA}}{{FB}} = \frac{{CA}}{{CB}},\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).
Khi đó \(\frac{{{S_{AEF}}}}{{{S_{ABC}}}} = \frac{{AE}}{{AC}}.\frac{{AF}}{{AB}} = \frac{{AB}}{{AB + BC}}.\frac{{AC}}{{AC + BC}}\), tương tự: \(\frac{{{S_{CED}}}}{{{S_{ABC}}}} = \frac{{CA}}{{CA + AB}}.\frac{{CB}}{{CB + AB}}\),\(\frac{{{S_{BFD}}}}{{{S_{ABC}}}} = \frac{{BC}}{{BC + CA}}.\frac{{BA}}{{BA + CA}}\).
Do đó
\({S_{DEF}} = {S_{ABC}}.\left( {1 - \frac{{ab}}{{\left( {a + c} \right)\left( {b + c} \right)}} - \frac{{bc}}{{\left( {b + a} \right)\left( {c + a} \right)}} - \frac{{ac}}{{\left( {a + b} \right)\left( {c + b} \right)}}} \right) = \frac{{2abc}}{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}.{S_{ABC}} = \frac{{210\sqrt 6 }}{{143}}\).
Suy ra: \({V_{S.DEF}} = \frac{1}{3}.\frac{{210\sqrt 6 }}{{143}}.2\sqrt 2 = \frac{{280\sqrt 3 }}{{143}}\,\left( {c{m^3}} \right) \approx 3,4\left( {c{m^3}} \right)\).
Chọn D.