Câu hỏi:
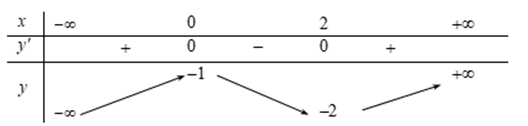
Cho hàm số liên tục trên và có bảng biến thiên như sau
Có bao nhiêu mệnh đề đúng trong số các mệnh đề sau đối với hàm số \(g\left( x \right)=f\left( 2-x \right)-2\)?
I. Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( -4;-2 \right).\)
II. Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( 0;2 \right).\)
III. Hàm số \(g\left( x \right)\) đạt cực tiểu tại điểm \(-2\).
IV. Hàm số \(g\left( x \right)\) có giá trị cực đại bằng \(A\).
- A 2
- B 3
- C 1
- D 4
Phương pháp giải:
Tính đạo hàm của hàm hợp, lập bảng biến thiên để xét tính đơn điệu và cực trị của hàm số
Lời giải chi tiết:
Từ bảng biến thiên ta có hàm số \(y=f\left( x \right)\), ta có
\({f}'\left( x \right)=0\)\(\Leftrightarrow \left[ \begin{align} & x=0 \\& x=2 \\\end{align} \right.\),\({f}'\left( x \right)>0\)\(\Leftrightarrow \left[ \begin{align} & x<0 \\& x>2 \\\end{align} \right.\), \({f}'\left( x \right)<0\Leftrightarrow 0<x<2\) và \(f\left( 0 \right)=-1\), \(f\left( 2 \right)=-2\).
Xét hàm số \(g\left( x \right)=f\left( 2-x \right)-2\) ta có \({g}'\left( x \right)=-{f}'\left( 2-x \right)\). Giải phương trình \({g}'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & 2-x=0 \\& 2-x=2 \\\end{align} \right.\).
Ta có \({g}'\left( x \right)>0\)\(\Leftrightarrow -{f}'\left( 2-x \right)>0\)\(\Leftrightarrow {f}'\left( 2-x \right)<0\)\(\Leftrightarrow 0<2-x<2\)\(\Leftrightarrow 0<x<2\).
Và \({g}'\left( x \right)<0\)\(\Leftrightarrow -{f}'\left( 2-x \right)<0\)\(\Leftrightarrow {f}'\left( 2-x \right)>0\)\(\Leftrightarrow \left[ \begin{align} & 2-x<0 \\& 2-x>2 \\\end{align} \right.\)\(\left[ \begin{align} & x>2 \\& x<0 \\\end{align} \right.\).
\(g\left( 0 \right)=f\left( 2-0 \right)-2\)\(=f\left( 2 \right)-2\)\(=-4\).
\(g\left( 2 \right)=f\left( 2-2 \right)-2\)\(=f\left( 0 \right)-2\)\(=-3\).
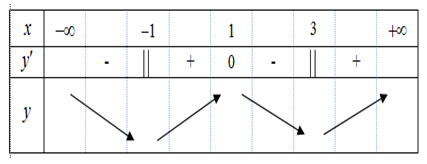
Bảng biến thiên
Từ bảng biến thiên ta có
Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( 0;2 \right)\) nên I sai.
Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( -\infty ;0 \right)\) và \(\left( 2;+\infty \right)\) nên II sai.
Hàm số \(g\left( x \right)\) đạt cực tiểu tại \(x=2\) nên III sai.
Hàm số \(g\left( x \right)\) đạt cực đại tại \(x=2\) và \({{g}_{C}}=g\left( 0 \right)\) nên IV đúng.
Chọn C