Câu hỏi:
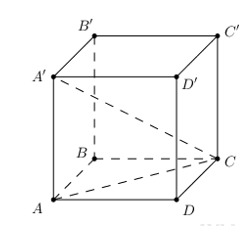
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Tính diện tích xung quanh của hình nón tròn xoay sinh bởi đường gấp khúc ACA’ khi quay quanh trục AA’.
- A \(\pi \sqrt 5 \)
- B \(\pi \sqrt 6 \)
- C \(\pi \sqrt 3 \)
- D \(\pi \sqrt 2 \)
Phương pháp giải:
Diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\) trong đó \(r;l\) lần lượt là bán kính và độ dài đường sinh của hình nón.
Lời giải chi tiết:
Ta có \(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta ACA'\) vuông tại A.
Khi quay tam giác ACA’ quanh cạnh AA’ ta được hình nón có đường cao \(AA' = 1\) và bán kính \(AC = \sqrt 2 \).
Khi đó độ dài đường sinh \(A'C = \sqrt 3 \).
Vậy diện tích xung quang của hình nón là \({S_{xq}} = \pi .AC.A'C = \pi .\sqrt 2 .\sqrt 3 = \pi \sqrt 6 \).
Chọn B.
Quảng cáo