Phương pháp giải:

- Xác định chân đường cao của đỉnh S đến mặt phẳng đáy.

- Tính thể tích khối chóp : \(V=\frac{1}{3}Sh\)

Lời giải chi tiết:

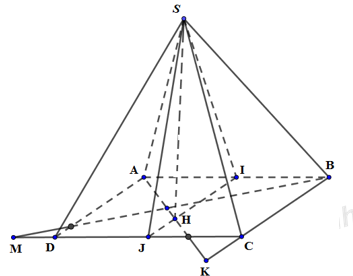
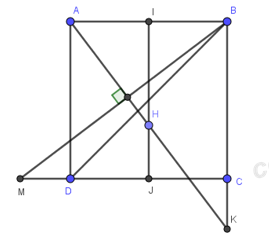
Gọi I, J lần lượt là trung điểm của AB, CD.

Tam giác SAB đều, tam giác SCD cân tại S nên \(SI\bot AB,\,\,SJ\bot CD\)

Mà AB//CD \(\Rightarrow AB,\,\,CD\bot \left( SIJ \right)\)

Dựng \(SH\bot IJ,\,\,(H\in IJ)\Rightarrow SH\bot (ABCD)\) (do \(SH\bot IJ\) và \(SH\subset \left( SIJ \right)\bot CD\))

Trong (ABCD), kẻ \(BM\bot AH,\,\,\left( M\in CD,\,AH\cap BM=T \right)\). Khi đó, điểm M thỏa mãn điều kiện đề bài.

+) \(\Delta SAB\)đều, cạnh a \(\Rightarrow SI=\frac{a\sqrt{3}}{2}\)

+) \(\Delta SCD\)vuông cân tại S, \(CD=a\Rightarrow SJ=\frac{CD}{2}=\frac{a}{2}\)

 +) ABCD là hình vuông cạnh a \(\Rightarrow IJ=a\)

Tam giac SIJ có: \(I{{J}^{2}}=S{{I}^{2}}+S{{J}^{2}}\Rightarrow \Delta SIJ\) vuông tại S.

Mà \(SH\bot IJ\Rightarrow S{{I}^{2}}=IH.IJ\Rightarrow {{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}=IH.a\Rightarrow IH=\frac{3a}{4}\)

Và \(\frac{1}{S{{H}^{2}}}=\frac{1}{S{{I}^{2}}}+\frac{1}{S{{J}^{2}}}=\frac{1}{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}+\frac{1}{{{\left( \frac{a}{2} \right)}^{2}}}=\frac{16}{3{{a}^{2}}}\Rightarrow SH=\frac{a\sqrt{3}}{4}\)

Dễ dàng chứng minh \(\Delta AIH\) đồng dạng tam giác \(\Delta BCM\Rightarrow \frac{{{S}_{AIH}}}{{{S}_{BMC}}}={{\left( \frac{AI}{BC} \right)}^{2}}=\frac{1}{4}\Rightarrow {{S}_{BCM}}=4{{S}_{AIH}}=4.\frac{1}{2}.\frac{a}{2}.\frac{3a}{4}=\frac{3{{a}^{2}}}{4}\)

\({{S}_{BDM}}={{S}_{BCM}}-{{S}_{BCD}}=\frac{3}{4}{{a}^{2}}-\frac{1}{2}{{a}^{2}}=\frac{{{a}^{2}}}{4}\)

Thể tích khối chóp S.BDM:  \({{V}_{S.BDM}}=\frac{1}{3}.SH.{{S}_{BDM}}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{{{a}^{2}}}{4}=\frac{\sqrt{3}{{a}^{3}}}{48}\)

Chọn: D