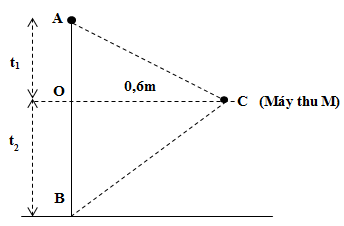
Câu hỏi:
Từ điểm A bắt đầu thả rơi tự do một điện tích điểm ở nơi có gia tốc g = 10m/s2, khi chạm đất tại B nó đứng yên luôn. Tại C cách đoạn thẳng AB 0,6m có một máy đo độ lớn cường độ điện trường. Biết khoảng thời gian từ khi thả điện tích đến khi máy thu M có số chỉ cực đại lớn hơn 0,2s so với khoảng thời gian từ đó đến khi máy thu M có số chỉ không đổi; đồng thời quãng đường sau dài hơn quãng đường trước là 0,2m. Bỏ qua sức cản của không khí và mọi hiệu ứng khác. Tỉ số giữa số đo đầu và số đo cuối của máy đo gần giá trị nào nhất sau đây?
- A 1,85
- B 1,92
- C 1,56
- D 1,35
Phương pháp giải:
Cường độ điện trường do điện tích điểm q gây ra: \(E = k{{\left| q \right|} \over {{r^2}}}\)
Quãng đường đi được của vật rơi tự do sau thời gian t: \(s = {{g{t^2}} \over 2} \Rightarrow t = \sqrt {{{2s} \over g}} \)
Lời giải chi tiết:
+ Độ lớn cường độ điện trường đo được ở máy thu M: \(E = k{{\left| q \right|} \over {{r^2}}} \Rightarrow {E_{m{\rm{ax}}}} \Leftrightarrow {r_{\min }} = OC \Rightarrow {E_{m{\rm{ax}}}} = {E_O}\)
+ Công thức tính quãng đường đi được của vật rơi tự do sau thời gian t là: \(s = {{g{t^2}} \over 2} \Rightarrow t = \sqrt {{{2s} \over g}} \)
+ Khoảng thời gian và quãng đường điện tích điểm đi được từ khi thả điện tích đến khi máy thu M có số chỉ cực đại là: \({t_1} = {t_{OA}} = \sqrt {{{2.OA} \over g}} ;{s_1} = OA\)
+ Khoảng thời gian và quãng đường điện tích điểm đi được từ khi máy thu M có số chỉ cực đại đến khi máy thu M có số chỉ không đổi là: \({t_2} = {t_{OB}} = {t_{AB}} - {t_{OA}} = \sqrt {{{2.AB} \over g}} - \sqrt {{{2.OA} \over g}} ;{s_2} = OB\)
+ Theo bài ra ta có:
\(\eqalign{
& \left\{ \matrix{
{t_1} - {t_2} = 0,2s \hfill \cr
{s_2} - {s_1} = OB - OA = 0,2m \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\sqrt {{{2.OA} \over g}} - \left( {\sqrt {{{2.AB} \over g}} - \sqrt {{{2.OA} \over g}} } \right) = 0,2 \hfill \cr
OB = OA + 0,2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2\sqrt {0,2.OA} - \sqrt {0,2.AB} = 0,2 \hfill \cr
AB = OA + OB = 2.OA + 0,2 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
2\sqrt {0,2.OA} - \sqrt {0,2.\left( {2.OA + 0,2} \right)} = 0,2 \hfill \cr
OB = OA + 0,2 \hfill \cr} \right. \Rightarrow \left\{ \matrix{
OA = \sqrt {0,8} \hfill \cr
OB = \sqrt {0,8} + 0,2 \hfill \cr} \right. \cr} \)
+ Cường độ điện trường tại A và B (số đo đầu và số đo cuối của máy thu):
\(\left\{ \matrix{
{E_A} = k{{\left| q \right|} \over {A{C^2}}} \hfill \cr
{E_B} = k{{\left| q \right|} \over {B{C^2}}} \hfill \cr} \right. \Rightarrow {{{E_A}} \over {{E_B}}} = {{B{C^2}} \over {A{C^2}}} = {{O{B^2} + O{C^2}} \over {O{A^2} + O{C^2}}} = {{{{\left( {\sqrt {0,8} + 0,2} \right)}^2} + {{0,6}^2}} \over {{{\left( {\sqrt {0,8} } \right)}^2} + {{0,6}^2}}} = 1,343\)