Câu hỏi:
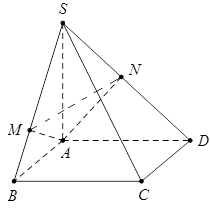
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) cạnh bên \(SA\) vuông góc với mặt phẳng đáy, \(SA=a\sqrt{2}.\) Gọi \(M,\,\,N\) lần lượt là hình chiếu vuông góc của điểm \(A\) trên các cạnh \(SB,\,\,SD\) (tham khảo hình vẽ bên). Góc giữa mặt phẳng \(\left( AMN \right)\) và đường thẳng \(SB\) bằng
- A
\({{45}^{0}}.\)
- B
\({{90}^{0}}.\)
- C
\({{120}^{0}}.\)
- D \({{60}^{0}}.\)
Phương pháp giải:
Lời giải chi tiết:

Ta có: \(\left\{ \begin{align} CD\bot SD \\ CD\bot SA \\ \end{align} \right.\Rightarrow CD\bot \left( SAD \right)\Rightarrow CD\bot AN.\)
Lại có \(AN\bot SD\Rightarrow SN\bot \left( SCD \right)\Rightarrow SN\bot SC.\)
Chứng minh tương tự ta được \(AM\bot SC.\)
Ta có: \(\left\{ \begin{align} AM\bot SC \\ AN\bot SC \\ \end{align} \right.\Rightarrow SC\bot \left( AMN \right)\)
Kẻ \(MH\bot SC\Rightarrow H\in \left( AMN \right)\Rightarrow SH\bot \left( AMHN \right)\)
\(\Rightarrow \widehat{\left( SB;\left( AMN \right) \right)}=\widehat{\left( SM;HM \right)}=\widehat{SMH}\)
\(\begin{align} \Delta SMH\backsim \Delta SCB\,\,\left( g.g \right)\Rightarrow \frac{MH}{BC}=\frac{SM}{SC} \\ \Rightarrow \frac{MH}{SM}=\frac{BC}{SC}=\frac{a}{\sqrt{2{{a}^{2}}+2{{a}^{2}}}}=\frac{1}{2}=\cos \widehat{SMH}\Rightarrow \widehat{SMH}={{60}^{0}} \\ \end{align}\)
Chọn D


















