Câu hỏi:
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính côsin của góc giữa mặt bên và mặt đáy.
- A \(\frac{1}{\sqrt{3}}\)
- B \(\frac{1}{2}\)
- C \(\frac{1}{\sqrt{2}}\)
- D \(\frac{1}{3}\)
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.
Lời giải chi tiết:
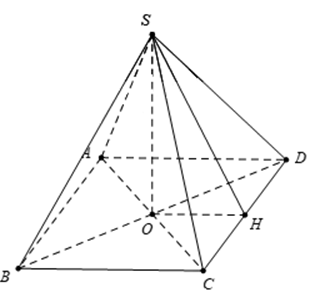
Dựng hình như hình vẽ.
Ta có: \(OA=\frac{a\sqrt{2}}{2}\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\frac{a\sqrt{2}}{2}\)
Gọi H là trung điểm của CD ta có :
\(\begin{array}{l}
\left\{ \begin{array}{l}
CD \bot OH\\
CD \bot SO
\end{array} \right. \Rightarrow CD \bot \left( {SOH} \right) \Rightarrow CD \bot SH\\
\left\{ \begin{array}{l}
\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\
\left( {SCD} \right) \supset SH \bot CD\\
\left( {ABCD} \right) \supset OH \bot CD
\end{array} \right. \Rightarrow \widehat {\left( {\left( {SCD} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SH;OH} \right)} = \widehat {SHO} = \varphi
\end{array}\)
Khi đó \(\tan \,\varphi =\tan \widehat{SHO}=\frac{SO}{OH}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a}{2}}=\sqrt{2}\)
Do đó \(c\text{os}\varphi =\frac{1}{\sqrt{{{\tan }^{2}}\varphi +1}}=\frac{1}{\sqrt{3}}\)
Đáp án A.