Phương pháp giải:

Diện tích toàn phần của hình trụ: \({{S}_{tp}}=2\pi Rh+2\pi {{R}^{2}}\)

Thể tích khối trụ \({{V}_{tru}}=Sh=\pi {{R}^{2}}h\), trong đó S: diện tích đáy, R: bán kính đáy, h: độ dài đường cao.

Lời giải chi tiết:

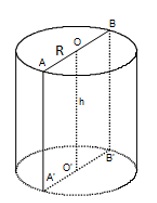
 \(\begin{array}{l}{S_{tp}} = 4\pi  \Leftrightarrow 2\pi Rh + 2\pi {R^2} = 4\pi  \Leftrightarrow 2\pi .\frac{{AB}}{2}.BB' + 2\pi {\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \\ \Leftrightarrow 2\pi .\frac{a}{2}.a + 2\pi {\left( {\frac{a}{2}} \right)^2} = 4\pi  \Leftrightarrow \frac{3}{2}{a^2} = 4 \Leftrightarrow a = \sqrt {\frac{8}{3}} \end{array}\)

(a : độ dài cạnh hình vuông ABB’A’).

Thể tích khối trụ:

\({{V}_{tru}}=\pi {{R}^{2}}h=\pi .{{\left( \frac{AB}{2} \right)}^{2}}.BB'=\pi {{\left( \frac{\sqrt{\frac{8}{3}}}{2} \right)}^{2}}.\sqrt{\frac{8}{3}}=\frac{4\sqrt{6}\pi }{9}\)

Chọn: B.