Phương pháp giải:

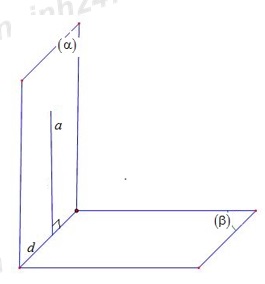
*)  \(\left\{ \begin{array}{l}\left( \alpha  \right) \bot \left( \beta  \right)\\\left( \alpha  \right) \cap \left( \beta  \right) = d\\a \subset \left( \alpha  \right)\\a \bot d\end{array} \right.\,\,\,\,\,\, \Rightarrow a \bot \left( \beta  \right)\)

*) Thể tích của khối chóp : \(V=\frac{1}{3}Sh\).

Trong đó, S: diện tích đáy, h: độ dài đường cao. 

Lời giải chi tiết:

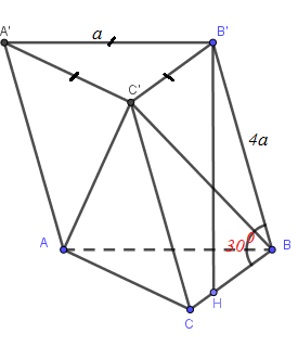
Ta có: \(\left\{ \begin{array}{l}(BCC'B') \bot (ABC)\\(BCC'B') \cap (ABC) = BC\end{array} \right.\)

Kẻ \(B'H\bot BC,\,\,H\in BC\Rightarrow B'H\bot (ABC)\).

Tam giác BB’H vuông tại H:

\(\sin \widehat{B'BH}=\frac{HB'}{BB'}\Leftrightarrow \sin {{30}^{0}}=\frac{HB'}{4a}\Rightarrow HB'=2a\)

Tam giác ABC đều, cạnh bằng a \(\Rightarrow {{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}\) \(\begin{array}{l}{V_{A.CC'B}} = {V_{C'.ABC}} = \frac{1}{3}d(C',(ABC)).{S_{ABC}} = \frac{1}{3}d(B',(ABC)).{S_{ABC}}\\ = \frac{1}{3}.B'H.{S_{ABC}} = \frac{1}{3}.2a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{6}\end{array}\)

Chọn: D.