Phương pháp giải:

- Sử dụng phương pháp tọa độ trong không gian.

Lời giải chi tiết:

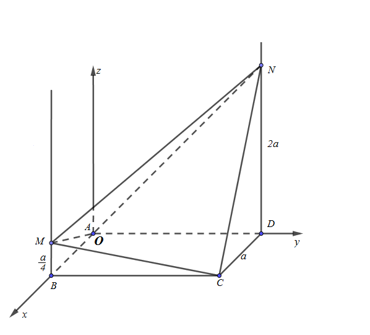
Gắn hệ trục tọa độ Oxyz:

\(\begin{array}{l}O \equiv A(0;0;0),\,\,\,\,B(a;0;0),\,\,\,C(a;a;0),\,\,\,\,D(0;a;0),\\M\left( {a;0;\frac{a}{4}} \right),\,\,\,\,N(0;a;2a)\end{array}\)

\(\begin{array}{l}\overrightarrow {AM}  = \left( {a;0;\frac{a}{4}} \right),\,\,\overrightarrow {AN}  = \left( {0;a;2a} \right)\\\overrightarrow {CM}  = \left( {0; - a;\frac{a}{4}} \right),\,\,\overrightarrow {CN}  = \left( { - a;0;2a} \right)\end{array}\)

Khi đó, (AMN) có 1 vectơ pháp tuyến là \(\overrightarrow{{{n}_{1}}}=\left[ \overrightarrow{{{u}_{1}}};\,\,\overrightarrow{{{u}_{2}}} \right]=(-1;-8;4)\) , trong đó: \(\overrightarrow{{{u}_{1}}}\left( 4;0;1 \right),\,\,\overrightarrow{{{u}_{2}}}\left( 0;1;2 \right)\)

             (CMN) có 1 vectơ pháp tuyến là \(\overrightarrow{{{n}_{2}}}=\left[ \overrightarrow{{{v}_{1}}};\,\,\overrightarrow{{{v}_{2}}} \right]=(-8;-1;-4)\) , trong đó: \(\overrightarrow{{{v}_{1}}}\left( 0;-4;1 \right),\,\,\overrightarrow{{{v}_{2}}}\left( -1;0;2 \right)\)

Ta thấy : \(\overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}}=(-1).(-8)+(-8)(-1)+4.(-4)=0\Rightarrow \varphi ={{90}^{0}}\).

Chọn: C.