Câu hỏi:
Diện tích lớn nhất \({{S}_{\max }}\)của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính \(R=6cm\)nếu một cạnh của hình chữ nhật nằm dọc đường kính của hình tròn mà hình chữ nhật đó nội tiếp.
- A \({{S}_{\max }}=36\pi \,c{{m}^{2}}.\)
- B \({{S}_{\max }}=36\,c{{m}^{2}}.\)
- C \({{S}_{\max }}=96\pi \,c{{m}^{2}}.\)
- D \({{S}_{\max }}=18\,c{{m}^{2}}.\)
Phương pháp giải:
Lời giải chi tiết:
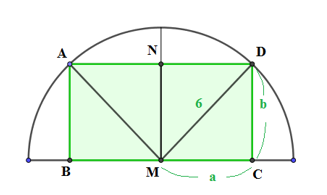
\({{S}_{ABCD}}=2{{S}_{CDNM}}=2.ab\overset{Cauchy}{\mathop{\le }}\,{{a}^{2}}+{{b}^{2}}={{6}^{2}}\Rightarrow {{S}_{\max }}=36\,(c{{m}^{2}})\) khi và chỉ khi \(a=b=3\sqrt{2}\,(cm)\).
Chọn: B.
Quảng cáo
Câu hỏi trước
