Phương pháp giải:

Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

Lời giải chi tiết:

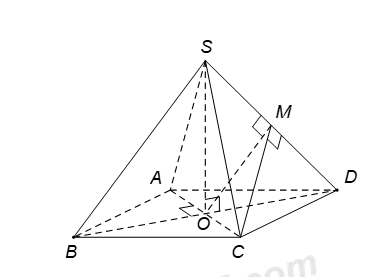
Gọi $O=AC\cap BD$. Do hình chóp $S.ABCD$ đều nên $SO\bot \left( ABCD \right)$.

Gọi M là trung điểm của SD. Tam giác SCD đều nên $CM\bot SD$.

Tam giác SBD có SB = SD = a, $BD=a\sqrt{2}$

Suy ra $\Delta \,SBD$ vuông tại $S\Rightarrow SB\bot SD\Rightarrow OM\bot SD.$

Do đó

$\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {SCD} \right) = SD\\\left( {SBD} \right) \supset OM \bot SD\\\left( {SCD} \right) \supset CM \bot SD\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {OM;CM} \right)} = \widehat {OMC}.$

Ta có $\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow OC \bot OM$.

Tam giác vuông MOC vuông tại O, có $\tan \widehat{CMO}=\frac{OC}{OM}=\frac{\frac{1}{2}a\sqrt{2}}{\frac{1}{2}a}=\sqrt{2}$.

Chọn D.