Câu hỏi:
Cho tam giác đều \(ABC\) cạnh \(a\). Gọi D là điểm đối xứng với \(A\) qua \(BC\). Trên đường thẳng vuông góc với mặt phẳng \(\left( ABC \right)\) tại \(D\) lấy điểm \(S\) sao cho \(SD=\dfrac{a\sqrt{6}}{2}\). Gọi \(I\) là trung điểm \(BC\); kẻ \(IH\) vuông góc \(SA\) \(\left( H\in SA \right)\). Khẳng định nào sau đây sai?
- A
\(SA\bot BH.\)
- B
\(\left( SDB \right)\bot \left( SDC \right).\)
- C
\(\left( SAB \right)\bot \left( SAC \right).\)
- D \(BH\bot HC.\)
Phương pháp giải:
Sử dụng các định lí về hai mặt phẳng vuông góc
Lời giải chi tiết:
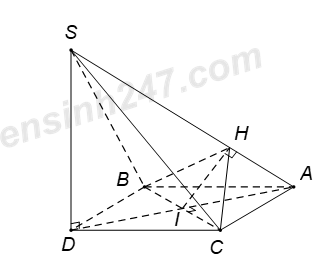
Từ giả thiết suy ra ABDC là hình thoi nên \(BC\bot AD.\)
Ta có \(\left\{ \begin{array}{l}BC \bot AD\\BC \bot SD\end{array} \right. \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SA\).
Lại có theo giả thiết \(IH\bot SA\). Từ đó suy ra \(SA\bot \left( HCB \right)\Rightarrow SA\bot BH\).
\(\Rightarrow \)Đáp án A đúng.
Tính được \(AI=\frac{a\sqrt{3}}{2}\), \(AD=2AI=a\sqrt{3}\), \(S{{A}^{2}}=\sqrt{A{{D}^{2}}+S{{D}^{2}}}=\frac{3a\sqrt{2}}{2}.\)
Ta có \(\Delta AHI\backsim \Delta ADS\Rightarrow \frac{IH}{SD}=\frac{AI}{AS}\Rightarrow IH=\frac{AI.SD}{AS}=\frac{a}{2}=\frac{BC}{2}\Rightarrow \) Tam giác \(HBC\) có trung tuyến \(IH\) bằng nửa cạnh đáy \(BC\) nên \(\widehat{BHC}={{90}^{0}}\) hay \(BH\bot HC\). Do đó D đúng.
Từ mệnh đề A và D suy ra \(BH\bot \left( SAC \right)\Rightarrow \left( SAB \right)\bot \left( SAC \right)\Rightarrow \) mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Chọn B


















