Câu hỏi:
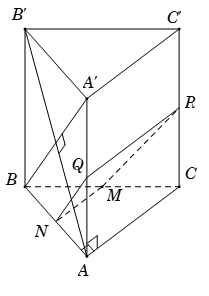
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\) với \(BC=a\sqrt{2}\); \(AA'=a\) và vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) qua \(M\) là trung điểm của \(BC\) và vuông góc với \(AB'\). Thiết diện tạo bởi \(\left( \alpha \right)\) với hình lăng trụ \(ABC.A'B'C'\) là:
- A Hình thang cân.
- B Hình thang vuông.
- C Tam giác.
- D Hình chữ nhật.
Phương pháp giải:
Lời giải chi tiết:
Gọi N là trung điểm \(AB\Rightarrow MN//AC\Rightarrow MN\bot AB\).
Ta có \(\left\{ \begin{align} & MN\bot AB \\ & MN\bot AA' \\\end{align} \right.\Rightarrow MN\bot \left( ABB'A' \right)\Rightarrow MN\bot AB'\Rightarrow MN\subset \left( \alpha \right).\)
Từ giả thiết \(\Rightarrow \)\(AB=a=AA'\Rightarrow ABB'A'\) là hình vuông \(\Rightarrow BA'\bot AB'\)
Trong mp \(\left( ABB'A' \right)\) kẻ \(NQ\parallel BA'\) với \(Q\in AA'\).
Trong mp \(\left( ACC'A' \right)\) kẻ \(QR\parallel AC\) với \(R\in CC'\).
Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và \(MN\bot NQ\)).
Chọn B.