Câu hỏi:
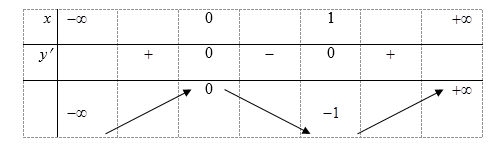
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên và có bảng biến thiên
Hỏi phương trình \(\left| {f\left( x \right)} \right| = \frac{2}{e}\) có bao nhiêu nghiệm thực phân biệt
- A \(4\).
- B \(2\).
- C \(3\).
- D \(1\).
Phương pháp giải:
Từ bảng biến thiên ta suy luận ra đồ thị hàm số y = f(x) sau đó ta vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) bằng cách như sau:
Bước 1: Vẽ đồ thị (C) của hàm số y = f(x)
Bước 2: Giữ nguyên đồ thị (C) phía trên trục hoành.
Bước 3: Lấy đối xứng với phần đồ thị (C) phía dưới trục hoành qua trục hoành (bỏ đi phần đồ thi phía dưới trục hoành)
Bước 4: Hợp 2 phần đồ thị trên chính là đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)
Lời giải chi tiết:
+) Đây là đồ thị hàm số bậc 3: \(y = a{x^3} + b{x^2} + cx + d\)
+) Đồ thị hàm số đi qua điểm (0;0) nên d = 0
+) Đồ thị hàm số đi qua điểm (1;-1) nên ta có: \(a + b + c = - 1\,\,\,\,(1)\)
\(y = a{x^3} + b{x^2} + cx + d \Rightarrow y' = 3a{x^2} + 2bx + c\)
Vì \(\left( {0;0} \right)\) là điểm cực đại của đồ thị hàm số nên \(x = 0\) là nghiệm của \(y' \Rightarrow c = 0\).
+) Đồ thị hàm số có điểm cực tiểu là (1;-1) nên \(x = - 1\) là nghiệm của \(y'\) ta có: \(3a + 2b = 0\)
Ta có hệ \(\left\{ \begin{array}{l}a + b + c = - 1\\c = 0\\3a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right.\)
Từ đó ta có hàm số cần tìm là: \(y = 2{x^3} - 3{x^2}\)
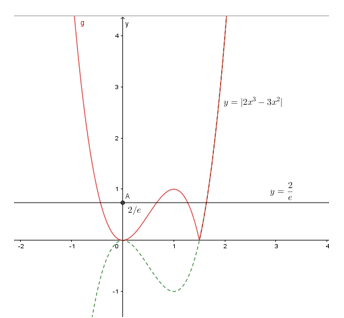
Vẽ đồ thị hàm số: \(y = \left| {2{x^3} - 3{x^2}} \right|\) ta được:
Dựa vào đồ thị hàm số ta có: Phương trình \(\left| {f\left( x \right)} \right| = \frac{2}{e}\) có 4 nghiệm thực.
Chọn đáp án A.