Câu hỏi:
Cho hình chóp S.ABC có SA ⊥ (ABC) và ∆ ABC vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác SBC. H là hình chiếu vuông góc của O lên mp(ABC). Khẳng định nào sau đây đúng?
- A H là trọng tâm tam giác ABC
- B H là tâm đường tròn nội tiếp tam giác ABC
- C H là trung điểm cạnh AC
- D H là trung điểm cạnh AB
Phương pháp giải:
Chứng minh H là trung điểm AB
Lời giải chi tiết:
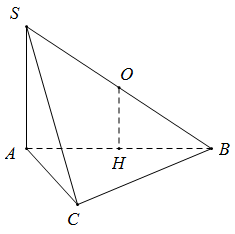
Ta có SA ⊥ (ABC) ⇒ SA ⊥ BC
Mà BC ⊥ AC nên BC ⊥ (SAC)
⇒ BC ⊥ SC
⇒ ∆ SBC vuông tại C
⇒ O là trung điểm SB
Vì SA ⊥ (ABC) nên (SAB) ⊥ (ABC)
⇒ OH ⊂ (SAB)
⇒ H ∈ AB
Trong mặt phẳng (SAB), ta có OH // SA, O là trung điểm SB ⇒ H là trung điểm AB
Chọn đáp án D
Quảng cáo
Câu hỏi trước
