Câu hỏi:
Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Gọi \(M,\, N\) lần lượt là trung điểm của \(BB’,\, CC’\). Mặt phẳng \((A’MN)\) chia khối lăng trụ thành hai phần, \({{V}_{1}}\) là thể tích của phần đa diện chứa điểm \(B\), \({{V}_{2}}\) là phần đa diện còn lại. Tính tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}.\)
- A \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\frac{7}{2}\)
- B \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=2\)
- C \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=3\)
- D \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\frac{5}{2}\)
Phương pháp giải:
Sử dụng công thức tính thể tích của khối chóp và tỉ lệ thể tích để làm bài toán.
Lời giải chi tiết:
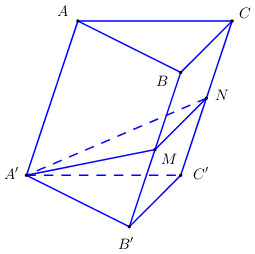
Vì \(M,\,\,N\) lần lượt là trung điểm của \(B{B}',\,\,\,C{C}'.\)
Suy ra \({{S}_{MN{C}'{B}'}}=\dfrac{1}{2}{{S}_{A'.BC{C}'{B}'}}\Rightarrow {{V}_{{A}'.MN{C}'{B}'}}=\dfrac{1}{2}{{V}_{BC{C}'{B}'}}=\dfrac{1}{2}\left( {{V}_{ABC.{A}'{B}'{C}'}}-{{V}_{{A}'.ABC}} \right)\)
Mà \({{V}_{{A}'.ABC}}=\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}\Rightarrow {{V}_{{A}'.MN{C}'{B}'}}=\dfrac{1}{2}\left( {{V}_{ABC.{A}'{B}'{C}'}}-\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}} \right)=\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}.\)
Vậy tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{V}_{{A}'MN.ABC}}}{{{V}_{{A}'.MN{C}'{B}'}}}=\dfrac{{{V}_{ABC.{A}'{B}'{C}'}}-\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}}{\dfrac{1}{3}{{V}_{ABC.{A}'{B}'{C}'}}}=2.\)
Chọn B.


















