Câu hỏi:
Trong hệ trục tọa độ Oxy cho A(-2; 0), B(-2; 2), C(4; 2), D(4; 0). Chọn ngẫu nhiên điểm có tọa độ (x; y) (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD (kể cả điểm nằm trên cạnh). Gọi A là biến cố “x, y đều chia hết cho 2”. Xác suất của biến cố A là:
- A \({7 \over {21}}\)
- B \({{13} \over {21}}\)
- C 1
- D \({8 \over {21}}\)
Phương pháp giải:
- Mô tả không gian mẫu.
- Liệt kê các khả năng có thể xảy ra của biến cố A.
- Tính sác xuất của biến cố A.
Lời giải chi tiết:
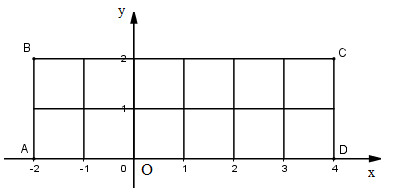
Ta có: \(\Omega = \left\{ {\left( {x,y} \right): - 2 \le x \le 4,0 \le y \le 2,x,y \in Z} \right\}.\)
\(\eqalign{ & x \in \left\{ { - 2; - 1;0;1;2;3;4} \right\},y \in \left\{ {0;1;2} \right\}. \cr & \Rightarrow {n_\Omega } = 7.3 = 21. \cr} \)
(Mỗi điểm là một giao điểm trên hình).
Ta có: A: “x, y đều chia hết cho 2” nên ta có \(A = \left\{ {\left( {x,y} \right):x \in \left\{ { - 2;0;2;4} \right\},y \in \left\{ {0;2} \right\}} \right\}.\)
Theo quy tắc nhân ta có: \({n_A} = 4.2 = 8.\)
Vậy \(P\left( A \right) = {{{n_A}} \over {{n_\Omega }}} = {8 \over {21}}.\)
Chọn D.


















