Câu hỏi:
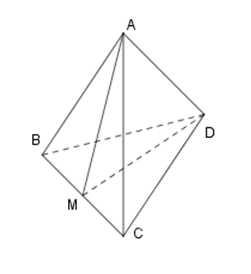
Cho tứ diện \(ABCD\) có \(AB=AC=2,\,DB=DC=3.\) Khẳng định nào sau đây đúng?
- A \(BC\bot AD.\)
- B \(AC\bot BD.\)
- C \(AB\bot \left( BCD \right).\)
- D \(DC\bot \left( ABC \right).\)
Phương pháp giải:
Phương pháp. Gọi \(M\) là trung điểm của \(BC.\) Chứng minh\(BC\bot \left( AMD \right)\Rightarrow BC\bot AD.\)
Lời giải chi tiết:
Lời giải chi tiết.
Gọi \(M\) là trung điểm của \(BC.\) Khi đó do \(\Delta ABC\) cân tại \(A\,\,\left( AB=AC \right)\)
Nên \(AM\bot BC\,\,\left( 1 \right).\)
Tương tự \(DM\bot BC\,\,\left( 2 \right)\) do tam giác \(\Delta BCD\) có \(BD=CD.\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(BC\bot \left( AMD \right)\Rightarrow BC\bot AD.\)
Chọn đáp án A.
Quảng cáo