Phương pháp giải:

Xác định hình chiếu của SC lên (ABCD).

Tính góc giữa SC và hình chiếu.

Lời giải chi tiết:

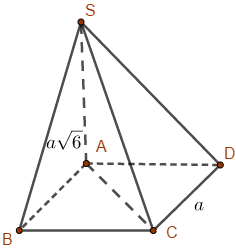
ABCD là hình vuông  cạnh a nên $AC = a\sqrt 2$

Ta có $SA \bot (ABCD)$ nên AC là hình chiếu của SC lên (ABCD). Vậy góc giữa SC và (ABCD) là góc giữa SC và AC và bằng $\widehat {SCA}$

$\begin{array}{l}\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{{a\sqrt 2 }} = \sqrt 3 \\ \Rightarrow \widehat {SCA} = 60^\circ \end{array}$