Phương pháp giải:

Giải ${x^2} + 4x + 3 = 0$.

Lập bảng xét dấu.

Lời giải chi tiết:

$\dfrac{{x - 1}}{{{x^2} + 4x + 3}} \ge 0$$\Leftrightarrow \dfrac{{x - 1}}{{\left( {x + 1} \right)\left( {x + 3} \right)}} \ge 0$

Bảng xét dấu:

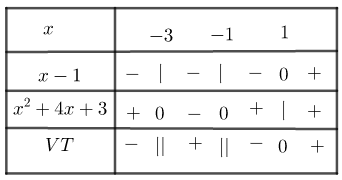
Từ bảng xét dấu ta có $S = \left( { - 3; - 1} \right) \cup \left[ {1; + \infty } \right)$

Phương pháp giải:

$\sqrt {f\left( x \right)}  \le g\left( x \right)$$\Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \ge 0\\f\left( x \right) \le {g^2}\left( x \right)\end{array} \right.$

Lời giải chi tiết:

$\begin{array}{l}\sqrt {2{x^2} - 5x + 2}  \le 2 - x\\ \Leftrightarrow \left\{ \begin{array}{l}2 - x \ge 0\\2{x^2} - 5x + 2 \ge 0\\2{x^2} - 5x + 2 \le {x^2} - 4x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\\left[ \begin{array}{l}x \ge 2\\x \le \dfrac{1}{2}\end{array} \right.\\{x^2} - x - 2 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 2\\x \le \dfrac{1}{2}\end{array} \right.\\ - 1 \le x \le 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\ - 1 \le x \le \dfrac{1}{2}\end{array} \right.\\ \Rightarrow S = \left\{ 2 \right\} \cup \left[ { - 1;\dfrac{1}{2}} \right]\end{array}$