Câu hỏi:
Cho tích phân \(I = \int\limits_0^3 {\frac{x}{{1 + \sqrt {x + 1} }}dx} \) nếu đặt \(t = \sqrt {x + 1} \) thì \(I = \int\limits_1^2 {f\left( t \right)dt} \) trong đó:
- A \(f\left( t \right) = 2{t^2} + 2t\)
- B \(f\left( t \right) = {t^2} - t\)
- C \(f\left( t \right) = 2{t^2} - 2t\)
- D \(f\left( t \right) = {t^2} + t\)
Phương pháp giải:
Đặt \(t = \sqrt {x + 1} \).
Đưa tích phân về biến t.
Tìm \(f\left( t \right)\)
Lời giải chi tiết:
Đặt \(t = \sqrt {x + 1} \Rightarrow {t^2} = x + 1\)\( \Rightarrow dx = 2tdt\).
Đổi cận:
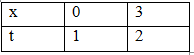
\(\begin{array}{l} \Rightarrow I = \int\limits_1^2 {\frac{{{t^2} - 1}}{{1 + t}}tdt} = \int\limits_1^2 {\left( {{t^2} - t} \right)dt} \\ \Rightarrow f\left( t \right) = {t^2} - t\end{array}\)
Quảng cáo
Câu hỏi trước
